104
Пошаговое объяснение:
Задание:
Найти m² +n², если m-n = 8 mn=20
Решение
1-й :
Составим систему уравнений:
m-n = 8 (1)
mn=20 (2)
Из (1) выразим m и подставим в уравнение (2):
m = 8 + n
(8 + n) · n=20
n² + 8n - 20 = 0
n₁,₂ = - 4±√(16+20) = - 4±6
n₁ = -4+6=2 m₁ = 20 : 2 = 10
n₂ = -4-6 = -10, m₂ = 20 : (-10) = -2
Таким образом:
m₁² +n₁² = 10² +2² = 100 + 4 =104
m₂² +n₂² = (-2)² + (-10)² = 4 + 100 =104
2-й :
Воспользуемся формулой:
a²+b² = (a - b)² + 2ab
m² +n² = (m - n)² + 2mn = 8² + 2· 20 = 104
ответ: m² +n² = 104
Пошаговое объяснение:
ДАНО: Y = x³/(x-1)
Исследование
1. Область определения: D(х)= R\{1} = (-∞;1)∪(1;+∞).
Не допускаем деления на 0 в знаменателе.
2.Поведение в точке разрыва. LimY(1-)= -∞, LimY(1+)= +∞. Вертикальная асимптота - х = 1. Неустранимый разрыв II-го рода.
3. Поведение на бесконечности - наклонная асимптота.
k = lim(+∞)Y(х)/x = х³/(x²+ x) = ∞ - коэффициент наклона.
Наклонной асимптоты нет.
4. Нули функции, пересечение с осью ОХ. Y(x) = 0.
5. Пересечение с осью ОУ. Y(0) = 0
6. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(0;1).
Положительна: Y>0 - X∈(-∞;0)∪(1;+∞)
7. Проверка на чётность.
Функция со сдвигом от осей симметрии - функция общего вида.
Ни нечётная: Y(-x) ≠ -Y(x) ни чётная: Y(-x) ≠ Y(x)
8. Поиск экстремумов по первой производной.
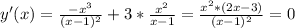
Корни квадратного уравнения. х1 = 0 и х2= 3/2 = 1,5.
9. Локальные экстремумы.
Минимум: Y(1,5) = 6.75 , Максимум: Y(0) = 0
10. Интервалы монотонности.
Возрастает: X∈(1.5;+∞)
Убывает: Х∈(-∞;1)∪(1;1.5)
11. Поиск перегибов по второй производной.
y''(x) = 2*x*(x²-3*x+3)/(x-1)² = 0
x = 0 и точка разрыва при Х = 1.
12. Выпуклая - 'горка' - X∈(0;1).
Вогнутая - 'ложка'- X∈(-∞;0)∪(1;+∞;).
13. Область значений. E(y) - y∈(-∞;+∞).
Рисунок с графиком функции в приложении.

------------------
4.25= 4 25/100=4 1/4 (четыре целых одна четвертая)