наверно ты имела ввиду что надо составить плоскость в которой лежат все три эти точки, привести его к общему виду и к виду в отрезках.
Чтобы найти уравнение плоскости, необходимо составить определитель вида
![\left[\begin{array}{ccc}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\\x-x_{1}&y-y_{1}&z-z_{1}\end{array}\right] =0](/tpl/images/0112/1221/de396.png) :
:
где соответствующие координаты принадлежать соответствующим точкам. Получаем:
![\left[\begin{array}{ccc}-1-1&0-2&4+1\\-2-1&-1-2&1+1\\x-1&y-2&z+1\end{array}\right] =0 \\ \\ \\ \left[\begin{array}{ccc}-2&-2&5\\-3&-3&2\\x-1&y-2&z+1\end{array}\right] =0 \\ \\ \\](/tpl/images/0112/1221/0862b.png)
Раскрываем определитель
![-2\left[\begin{array}{cc}-3&2\\y-2&z+1\end{array}\right] +2\left[\begin{array}{cc}-3&2\\x-1&z+1\end{array}\right] + 5\left[\begin{array}{cc}-3&-3\\x-1&y-2\end{array}\right] = 0](/tpl/images/0112/1221/569c5.png)
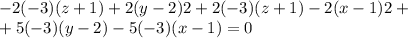
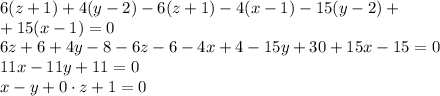 ]
]
x-y+1 = 0 Искомое уравнение плоскости, из-за коэфициента при координате z равного нулю, координата z не учитывается в уравнении. Плоскость параллельна оси Оz.
Приведем уравнение плоскости из общего вида к виду в отрезках. Уравнение в отрезках имеет вид
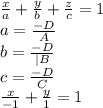
4,5m+1,9n+3,3m+4,3n=7,8m+6,2n