Пошаговое объяснение:
1 Задание.
Вспоминаем или узнаем одно из свойств корней:
![\sqrt[n]{x^p} = x^{\frac{p}{x} }](/tpl/images/1344/5744/b4c77.png)
, тогда в первом задании:
![\sqrt[4]{a} : a ^ \frac{1}{2} = a ^ \frac{1}{4} : a ^ \frac{1}{2}](/tpl/images/1344/5744/47562.png)
Теперь вспоминаем свойство степеней при делении:
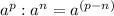, тогда выходит:
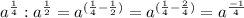
Вернем 4 на место
![a ^ \frac{-1}{4} = \sqrt[4]{a ^ {(-1)}}](/tpl/images/1344/5744/95027.png)
, мы можем вытащить степень за корень и получим:
![(\sqrt[4]{a}) ^ {-1}](/tpl/images/1344/5744/64355.png)
возведение в отрицательную степень: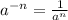 
В нашем случае: ![(\sqrt[4]{a}) ^ {-1} = \frac{1}{\sqrt[4]{a} }](/tpl/images/1344/5744/b0179.png)
. ответ: 3
2 Задание:
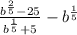, Здесь используем формулу сокращенного умножения:
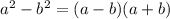
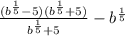, сокращаем одну скобку и у нас остается
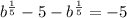. ответ: 1) -5
3 Задание:
Ну что, вспоминаем формулы по логарифмам:
log
b = c
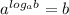
Нам это подходит для последнего, где 5. То есть,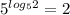 
Вспоминаем или узнаем еще одну формулу:
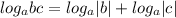
В нашем случае:
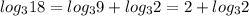, Мы знаем чтобы получить из 3 9, нужно возвести её во вторую степень, поэтому так и выходит. Теперь все соединяем и получаем:
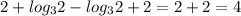. ответ 3) 4
Ну вот и все объяснения
