Всего возможны две ситуации: из конверта в конверт будет переложена простая задача или задача повышенной сложности.
Рассмотрим случай, когда будет переложена простая задача.
Найдем вероятность того, что из первого конверта во второй будет переложена простая задача. Для этого разделим число простых задач на общее количество задач в первом конверте:
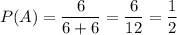
После такого перекладывания во втором конверте окажется 5 простых задач и 8 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
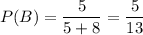
Но такой конверт получается только с вероятностью 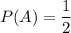 . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
. Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
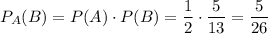
Рассмотрим случай, когда будет переложена задача повышенной сложности.
Найдем вероятность того, что из первого конверта во второй будет переложена задача повышенной сложности:
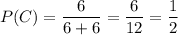
После такого перекладывания во втором конверте окажется 4 простые задачи и 9 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
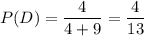
Но такой конверт получается только с вероятностью 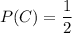 . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
. Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
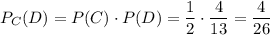
Поскольку события "переложить простую задачу" и "переложить задачу повышенной сложность" - несовместные, то общая вероятность достать простую задачу:
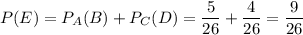
ответ: 9/26
В точке х=5 функция принимает наименьшее значение -1
Пошаговое объяснение:
Сначала найдем значения функции на концах отрезка
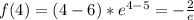
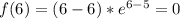
Теперь исследуем функцию на наличие экстремума в пределах отрезка.
Найдем ее производную, как производную произведения
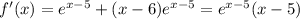
Приравниваем производную к нулю
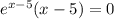
Показательная функция не может быть равна нулю, поэтому нулю равна скобка, т.е. х=5 - локальный экстремум. Исследуем как меняется знак производной в этой точке
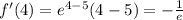 - функция убывает
- функция убывает
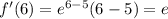 - функция возрастает, значит точка х=5 - точка минимума функции. Значение функции в этой точке
- функция возрастает, значит точка х=5 - точка минимума функции. Значение функции в этой точке
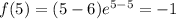
Из всех трех значений, именно это наименьшее. Значит функция принимает наименьшее значение -1 в точке x=5. Подкреплю свои расчеты графиком.
![15) Найдите наименьшее значение функции на отрезке [4;6]](/tpl/images/1358/0629/5777c.jpg)
10+10=20м2 - площадь 2 грядок
20*30=600 кг - огурцов с 2 грядок
ответ: 600 кг огурцов