Пошаговое объяснение:
Ромб - параллелограмм у которого все стороны равны .
Теорема : Диагонали ромба пересекаются под прямым углом и лежат на биссектрисах его углов
Доказательство :
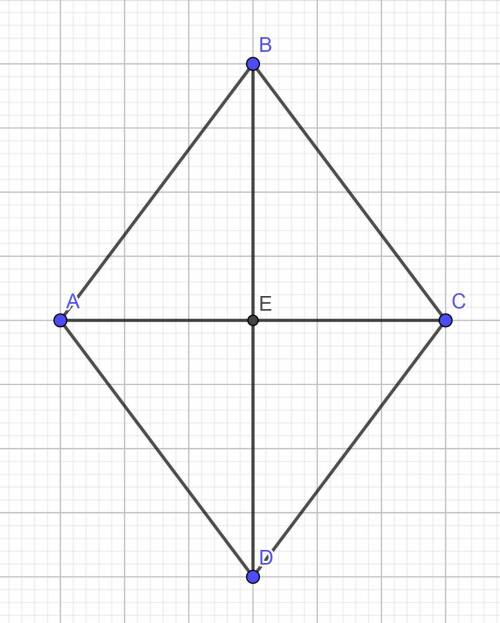
Нарисуем ромб АВСД ( рисунок во вложении ) .Рассмотрим ΔАВD . Поскольку у ромба все стороны равны , то АВ=AD , а это значит , что ΔABD - равнобедренный .Поскольку ромб это параллелограмм , значит диагонали в точке пересечения делятся пополам, т.е. ВЕ=ЕD. По-этому можно утверждать , что АЕ - это медиана (отрезок соединяющий вершину с серединой противоположной стороны) , а по свойству равнобедренного треугольника : медиана, проведенная к основанию, является биссектрисой и высотой, а значит АЕ - высота и биссектриса Δ АВD. Следовательно АЕ⊥BD и угол ВАЕ = углу DAE, что говорит о том , что диагонали ромба пересекаются под прямым углом и лежат на биссектрисах его углов.
Если да, то вот:
1) 28+48=76;
2) 76*7=532.
(28+48)*7=532.
А если 28+48*7, то вот:
1) 48*7=336;
2) 28+336=364.
28+48*7=364.