Квадрат разделили на 2 четырехугольника, один из которых квадратом не является, и 5 прямоугольных треугольников.
Определили фигуры с прямыми углами и раскрасили их.
Пошаговое объяснение:
Требуется определить, на какие фигуры разделили квадрат.
Также надо раскрасить фигуры с прямыми углами.
Вспомним определение квадрата и прямоугольного треугольника:
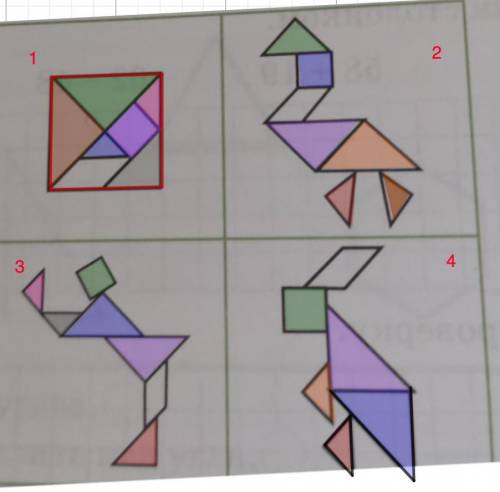
Квадрат — правильный четырёхугольник, у которого все стороны равны и все углы прямые.Прямоугольный треугольник – треугольник, у которого один угол – прямой, т.е. равный 90°.1. На 1 рисунке квадрат разделили на несколько фигур, одна из которых (сиреневая) - квадрат, остальные раскрашенные фигуры - прямоугольные треугольники.
Одна нераскрашенная фигура - четырехугольник, который не является квадратом, так как не имеет прямых углов.
2. На втором рисунке мы найдем также один квадрат и 5 прямоугольных треугольников.
Один нераскрашенный четырехугольник не является квадратом.
3. На 3 рисунке - 1 квадрат и 5 прямоугольных треугольников. И тоже есть четырехугольник, не являющийся квадратом.
4. На 4 рисунке есть 1 квадрат и 4 прямоугольных треугольника.
Нераскрашенная фигура - четырехугольник, который квадратом не является.
Определили фигуры с прямыми углами и раскрасили их.
Прибавили -2022 к обеим сторонам равенств, получили:
а) 2020 + 2 + ( -2022 ) = 2022 + ( -2022) = 0.
b) -1 + 23 + ( -2022 ) = 22 + ( -2022 ) = -2000.
Пошаговое объяснение:
Если к обеим частям верного числового равенства прибавить одно и то же число, получим верное числовое равенство.
а) 2020 + 2 = 2022
Прибавим к обеим частям -2022, число за знаком "минус", значит его заключаем в скобки. Перед скобками стоит знак "плюс", значит скобки можно опустить, сохраняя знак "минус".
2020 + 2 + ( -2022 ) = 2022 + ( -2022) = 2022 - 2022 = 0.
b) - ( + ( + ( - ( -1 )))) + 23 = 22
-1 + 23 + ( -2022 ) = 22 + ( -2022 ) = 22 - 2022 = -2000
....................................................................................................................
Более подробное решение:
Чтобы сложить числа разных знаков, нужно из большего модуля вычесть меньший и полученную разность записать со знаком того слагаемого, модуль которого больше.
а) 2020 + 2 + ( -2022 ) = 2022 + ( -2022)
2022 + ( -2022 ) = 2022 + ( -2022 )
2022 - 2022 = 2022
0 = 0
b) -1 + 23 + ( -2022 ) = 22 + ( -2022 )
23 - 1 + ( -2022 ) = 22 + ( -2022 )
22 + ( -2022 ) = 22 + ( -2022 )
22 - 2022 = 22 - 2022
- ( 2022 - 22 ) = - ( 2022 - 22 )
-2000 = -2000
