1) зачеркнули 7 из числа 17;
2) зачеркнули 8 из числа 85.
Решение 1:Искомое двузначное число представим в виде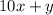 
(
и 
- однозначные и неотрицательные, при этом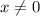 
).
1). Пусть зачеркнули цифру из разряда десятков. Тогда из числа 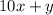получилось число . Нам нужно выполнение следующего равенства:
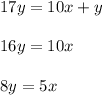
Единственные однозначные натуральные решения: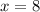 
и 
.
Значит, число 
⇒ 
.
2). Пусть зачеркнули цифру из разряда единиц. 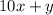⇒ . Уравнение составляется и решается по аналогии:
Откуда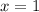 
и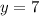 
.
Имеем второе подходящее решение: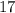 
⇒ 
.
Значит, двузначное число - это 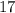или , или .
Можно было и кратким подбором решить, умножая все цифры на 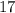(умножаемая цифра - та, которая могла остаться после вычеркивания), пока не станут появляться трехзначные числа.
Нам нужно, чтобы в получившемся числе присутствовало умножаемое число (иначе как оно смогло бы потом остаться?):
- не подходит, не двузначное.
- подходит, вычеркивали 
из числа .
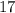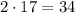- не подходит.
- не подходит.
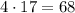- не подходит.
- подходит, вычеркивали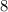 
из числа .
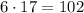- не подходит, начинаются трехзначные числа.
Получаем те же самые два решения: 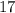и .
Пусть х км — искомое расстояние. Чтобы пройти это расстояние путнику, идущему со скоростью 2,5 км/ч, необходимо дробь, числитель — x, знаменатель — { 2,5} часа. Второй путник движется со скоростью 3 км/ч, поэтому чтобы пройти 1,1 км до опушки и вернуться на 1,1 минус x км назад, ему необходимо дробь, числитель — 1,1, знаменатель — 3 + дробь, числитель — 1,1 минус x, знаменатель — 3 часа. Времена движения путников равны, тогда:
дробь, числитель — x, знаменатель — { 2,5} = дробь, числитель — 1,1, знаменатель — 3 плюс дробь, числитель — 1,1 минус x, знаменатель — 3 равносильно дробь, числитель — 3x, знаменатель — 2,5 умножить на 3 = дробь, числитель — 5,5 минус 2,5x, знаменатель — 2,5 умножить на 3 равносильно 3x = 5,5 минус 2,5x равносильно 5,5 x = 5,5 равносильно x=1.
Тем самым, искомое расстояние равно 1 км.
14.737-11.751-к=715
2.986-к=715
-к=715-2.986
-к=712.014
к=-712.014
2) 14.737-11.751+к=715
2.986+к=715
к=715-2.986
к=712.014