Прямоугольник у нас равнобедренный, т.к. АС=ВС. Опустим медиану=биссектрису из вершины С на сторону АВ. Точку пересечения с АВ обозначим D. Тогда Получим прямоугольный треугольник АСD. Сторона АD=10, AC=26, CD (считаем по т.Пифагора)=24. Смежный угол равен 180°-∠САD.
tg(180°-∠САD) = sin(180°-∠САD)/cos(180°-∠САD) = sin(∠САD)/-cos(∠САD)
sin и cos ищем при нашего прямоугольного треугольника ACD:
sin(∠САD)=CD/AC (противолежащ. сторона к гипотенузе) = 24/26
cos(∠САD)=AD/AC (прилежащ. сторона к гипотенузе) = 10/26
подставляем, не забывая про минус в знаменателе (перенесу в числитель и сразу переверну дробь, на которую делим):
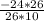
сокращаем, получаем: tg=-2,4
22-7= 93-4= 28+9= 32-7 = 73-4= 38+9= 42-7 = 53-4= 48+9=: 22-7=15 33-4=29 28+9=37 32-7=25 43-4=39 38+9=47 42-7=35 53-4=49 48+9=57 52-7=45 63-4=59 58+9=67 62-7=55 73-4=69 68+9=77