4. Из основного тригонометрического тождества:
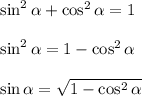
Так как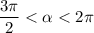 
, то 
.
.
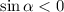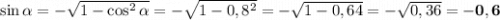ответ: -0,6
5.
![\sqrt[6]{\left(m-n\right)^6} - \sqrt[4]{m^4} = \left|m-n\right| - \left|m\right|](/tpl/images/1874/3421/381cf.png)
Так как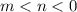 
, то модуль будет раскрываться вот так:
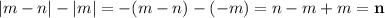
ответ: n
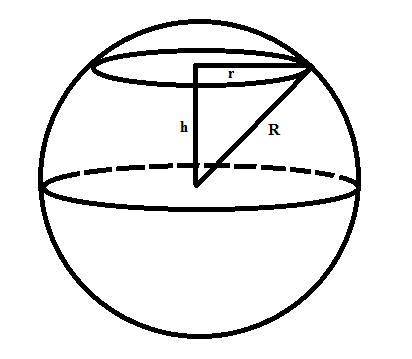
6. (см. чертёж во вложении) Сечение шара представляет собой круг. Площадь круга задаётся формулой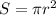 
, отсюда:
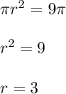
Получается прямоугольный треугольник, где гипотенуза - это радиус шара, один катет - радиус сечения, второй катет - расстояние от центра шара до сечения. По теореме Пифагора:
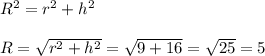
Формула объёма шара: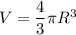 
. Подставляем известные значения:
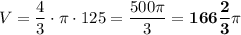
ответ: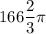 
7.
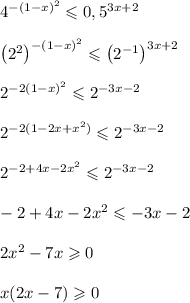
Решим неравенство методом интервалов.
Нули: 0; 3,5
+ - +
--------------------
----------------------------------------> x
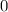
Так как в последней строке неравенства стоит знак "больше или равно", нам подходят те промежутки, где стоит знак "плюс".
ответ: ![x\in\left(-\infty;\ 0\right]\cup\left[3,5;+\infty\right)](/tpl/images/1874/3421/1b59b.png)
.
1. Проведём в трапеции АВСД отрезок АС:
АС ⊥ АД
2. Рассмотрим треугольник АБС:
Треугольник АБС — равнобедренный и прямоугольный, значит углы ВАС и ВСА равны:
ВАС = ВСА = (180 - 90)/2 = 45°
3. Т.к. угол ВСА = 45°,
то угол АСД = 105 - 45 = 60°
4. Рассмотрим треугольник АСД:
Треугольник АСД — прямоугольный,
угол АСД = 60°
Катет, лежащий против угла в 60° (то есть АД) равен половине гипотенузы:
АД =
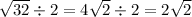
Тогда АС² по теореме Пифагора равно:
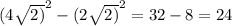
5. Вернёмся к треугольнику АБС:
По т. Пифагора АС² = х² + х² = 2х²
х² = АС²/2 = 12
х = √12 = 2√3
ответ: 2√3
6-победы;
2-пораженияж
Ничьи-?
1)12-6=6-не побед.
2)6-2=4-ничьи.
ответ: 4 ничьи