нет, если n и k - натуральные числа!
Пошаговое объяснение:
Воспользуемся таким свойством: квадрат натурального (или целого) числа при делении на 3 дает остаток 0 или 1.
7 в любой натуральной степени при делении на 3 дает остаток 1
в качестве доказательства можно сделать следующее:
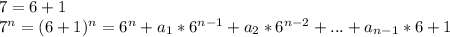
каждое слагаемое, кроме последнего делится на 6, а значит делится и на 3. Последнее слагаемое (единица) при делении на 3 дает остаток 1.
Значит все выражение при делении на 3 дает остаток 1.
Таким образом 7ⁿ можно переписать как 3a+1, a∈N (3 a показывает, что число делится на 3; 1 означает, что получается остаток 1)
Также 7^k=3b+1, тогда
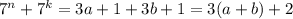
первое слагаемое делится на 3, а второе означает остаток.
То есть если 7^n+7^k поделить на 3, получится остаток 2, что невозможно для квадрата целого числа!
2 сплав. Марганца 3у кг, алюминия 16у, меди 181у. Всего 200у кг.
И массы одинаковы
22x=200y; 11x=100y.
Известно, что во 2 сплаве одного из металлов на 87,3 кг больше.
1) Пусть этот металл - марганец.
3y=x+87,3; x=3y-87,3; подставляем
11(3y-87,3)=100y
33y-960,3=100y
y<0 - не подходит.
2) Пусть этот металл - алюминий.
16y=4x+87,3; x=4y-21,825
11(4y-21,825)=100y
44y-240,075=100y
y<0 - не подходит.
3) Значит, этот металл - медь.
181y=17x+87,3; x=(181y-87,3)/17
11/17*(181y-87,3)=100y
11*181y-11*87,3=1700y
1991y-1700y=960,3
y=960,3/291=3,3 кг.
Масса сплава 100y=330 кг.