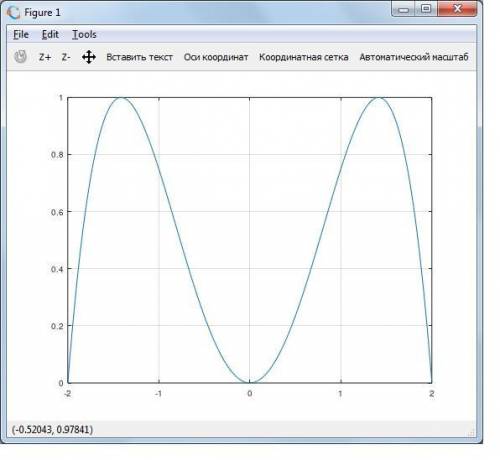
1. Область определения x ∈(-∞,+∞), функция - чётная
2. y' = -x³+2x
3. y'=0, 2x-x³=0, x(2-x²)=0, стационарные точки x=0, x=±
4. y'>0, x>0, x< , x∈(0,
, x∈(0,
y'>0, x<0, x< - , x∈(-∞,-
, x∈(-∞,-
Тогда промежуток возрастания x ∈(-∞,- )∪(0,
)∪(0,
Промежуток убывания x ∈ (- ,0)∪(
,0)∪(
В точке x = 0, производная меняет знак с минуса на плюс, то есть x=0 - точка минимума
в окрестности точек x=± производная меняет знак с плюса на минус, это точки максимума
производная меняет знак с плюса на минус, это точки максимума
y(0)=0
y(± )=2-1=1
)=2-1=1
вот и график, построенный в Октаве
Пошаговое объяснение:
ответ: y = -3x + 1,5
Пошаговое объяснение:
Скласти рівняння дотичної до графіка функції у точці
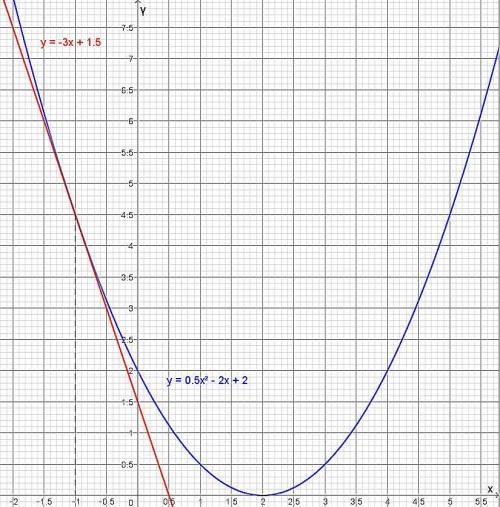
y= 0,5x² − 2x + 2, x₀= −1
Составить уравнение касательной к графику функции в точке
y=0,5x²−2x+2, x₀=−1
Запишем уравнения касательной в общем виде:
y = y₀ + y'(x₀)(x - x₀)
По условию задачи x₀ = -1, тогда
y₀ = у(-1) = 0,5·1² - 2·(-1) + 2 = 4,5
Теперь найдем производную:
y' = (0,5x² - 2x + 2)'= x - 2
следовательно:
y'(-1) = (-1) - 2 = -3
В результате уравнение касательной:
y = 4,5 - 3(x - (-1))
или
y = -3x + 1,5
Рішення:
Запишемо рівняння дотичної в загальному вигляді:
y = y₀ + y'(x₀)(x - x₀)
За умовою задачі x₀ = -1, тоді
y₀ = у(-1) = 0,5·1² - 2·(-1) + 2 = 4,5
Тепер знайдемо похідну:
y' = (0,5x² - 2x + 2)'= x - 2
отож:
y'(-1) = (-1) - 2 = -3
В результаті рівняння дотичної:
y = 4,5 - 3(x - (-1))
або
y = -3x + 1,5
1
19/25-(21/50+2/25)-6/25
Сначала работаем над скобкой.
Ищем общий знаменатель для 21/50+2/25
21+4/50
25/50
1/2
Теперь решаем.
19/25-1/2-6/25
19-6/25-1/2
13/25-1/2
Ищем общий знаменатель.
26-25/50
1/50
0,02
2
27/129+(12/86-6/43)-7/43
Работаем над скобкой.
12/86-6/43
Сокращаем 12/86 на 2
6/43-6/43
0
Теперь решаем.
27/129+0-7/43
27/129-7/43
Сокращаем 27/129 на 3
9/43-7/43
2/43≈0,04