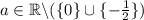Заметим, что, если x₀(a) - решение данного уравнения, то -x₀(a) также является решением уравнения. Поэтому при всех a таких, что x≠0, уравнение имеет не менее двух решений. Отсюда легко вывести, что a≠0;
Сделаем замену: m=x²; Так как m+m²≥0, то исходное уравнение (относительно m) равносильно следующему:
; Мы видим, что уравнение имеет единственное решение относительно m для данного a (при всех a, при которых выражение имеет смысл); Значит уравнение относительно x имеет ровно два решения. Осталось рассмотреть случай:
Выражение имеет смысл (рассматриваем дробь), если числитель равен, больше или меньше нуля, а знаменатель не равен нулю. Числитель: ( - X^2 - X + 2 ) D = 1 - 4*(-1)*2 = 9 ( V D = 3 ) X1 = ( 1 + 3 ) \ - 2 = - 2 X2 = - 2 \ - 2 = + 1 Запишем числитель: ( Х + 2 ) * ( X - 1 ) Знаменатель не равен нулю: X^2 - 4 = (X - 2)*(X + 2) После сокращения, получаем дробь: ( Х - 1 ) \ ( Х - 2) (Х - 2 ) не равен 0 --> Х не равен 2 Значит, выражение имеет смысл, если Х равен 1, больше (или меньше 1). Не имеет смысла, если Х равен 2
Берешь 5 литровое ведро, наливаешь из него 5 литров в 9 литровое ведро, снова берешь 5 литровое ведро и льешь в 9 литровое- войдет 4 литра, а 1литр останетсяИли можно по другому влить два раза по 5 литров в бочку, отлить из нее 9литров=1литр Из 9литрового ведра выливаешь в 5литровое 5 литров, остается 4 литра, если отлить половину=2литра Или по другому вбочку льем 5+5+5+5=20л отливаем из бочки два раза в 9 литровые. получаем 2 литра в бочке осталось т.е 5+5+5+5-9-9=2 Берем в бочку два раза наливаем из 9 литрового=18л в бочке ,выливаем 5 литров=13 литров еще раз выливаем 5 литров=3 литра т.е.9х2-5-5=3 удваиваем это решение, 4 раза наливаем из 9 литрового и шесть раз выльем по 5 литров 9х4-5-5-5-5-5-5=6литров удачи!
Заметим, что, если x₀(a) - решение данного уравнения, то -x₀(a) также является решением уравнения. Поэтому при всех a таких, что x≠0, уравнение имеет не менее двух решений. Отсюда легко вывести, что a≠0;
Сделаем замену: m=x²; Так как m+m²≥0, то исходное уравнение (относительно m) равносильно следующему:
1+2a≠0 ⇔ a≠-0.5;
ОТВЕТ: