гимнастика в дореволюционной россии
различные гимнастические были известны еще в древней руси - как составная часть народных праздников.
широкое развитие гимнастики в россии началось в xviii веке. серьезное внимание гимнастике, как прикладной дисциплине, уделял петр i и а.в. суворов. содержание внедрявшихся - по его инициативе - в армии гимнастических суворов изложил в полковом учреждении.
как и в других странах, в россии спортивная гимнастика первоначально культивировалась в основном в армейской среде. в 70-е годы xix в известный российский ученый и педагог п.ф. лесгафт открывает в санкт-петербурге двухгодичные гимнастические курсы (ныне - институт культуры им. лесгафта). первые в нашей стране соревнования по гимнастике, организованные гимнастическим обществом, прошли в 1885 г. в москве. в них приняли участие всего 11 человек, но начало было положено.
в 1889 г. гимнастика вводится в программу мужских учебных заведений. в конце xix - начале xx века в различных городах россии гимнастические общества и кружки, начинают регулярно проводиться чемпионаты страны.
в 1912 г. российские гимнасты впервые приняли участие в олимпийских играх, но составить конкуренцию более опытным соперникам не смогли.
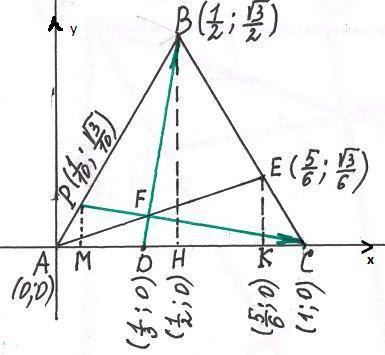
В равностороннем треугольнике ABC на сторонах AC и BC отметили точки D и E такие, что CD=2AD, BE=2CE. Обозначим точку пересечения отрезков AE и BD через F. Чему равен угол BFC?
Пошаговое объяснение:
1) Введем прямоугольную систему координат .Пусть АВ=ВС=АС=1. Пусть FC∩АВ=Р .Пусть ЕК⊥АС, ВН⊥АС, РМ⊥АС.
2) Определим координаты точек .
А(0;0) ,В(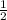 ;
;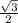 ) ,С(1;0) ,Н(0,5 ;0) ,D(
) ,С(1;0) ,Н(0,5 ;0) ,D( 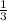 ;0) ,К(
;0) ,К( 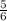 ;0) , Е(
;0) , Е(
3)Найдем координаты направляющих векторов: DB( 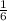 ;
;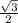 ) , РС(
) , РС( 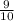 ;
;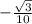 ).
).
4)Найдем скалярное произведение векторов .
DB *РС= 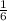 *
* 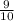 +
+ 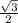 *(
*(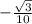 ) =
) =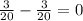 ⇒вектор DB⊥PC ⇒∠BFC=90°.
⇒вектор DB⊥PC ⇒∠BFC=90°.
=======================================
Пояснения( жуткие вычисления , слабонервным можно не читать).
1) Координаты точки Е. ΔКСЕ прямоугольный .
КЕ=СЕ*sin60= 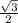 *
* 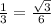 .
.
КС=СЕ*cos60= 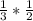 =
=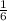 , поэтому АК= 1-
, поэтому АК= 1-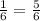 → Е(
→ Е( 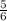 ;
;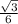 ) .
) .
2)Координаты точки В. ΔАВН- прямоугольный .
АН=НС= 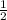 .
.
ВН=АВ*sin60=1* 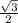 =
=
3)Ищем координаты точки Р
а)ΔВDC , по т. Менелая 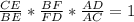 ,
, 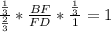 ,
, 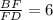 .
.
б)ΔАВD , по т. Менелая 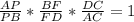 ,
, 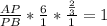 ,
, 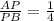 ,
,
AP=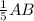 =
= 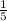 .
.
в)ΔАРМ прямоугольный .
РМ=АР*sin60=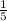 *
* 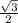 =
= 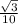 .
.
АМ=АР*cos60= 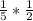 =
=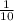 → P (
→ P ( 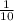 ;
;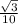 ) .
) .
Удачи!