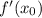
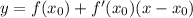
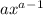- где а- степень
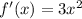- вот такая вот производная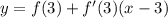
:
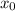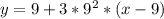
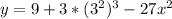
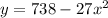
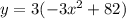- это и есть касательная в ДАННОЙ точке.
Представить число 7 в виде суммы трех натуральных слагаемых можно следующими с точностью до порядка слагаемых):
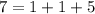
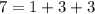
Представления первыми двумя не могут соответствовать сторонам треугольника, так как для них не выполняется неравенство треугольника. Заметим, что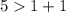 
и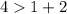 
, хотя каждая сторона треугольника должна быть меньше суммы двух других сторон.
Значит, треугольник имеет стороны 1, 3, 3 или 2, 2, 3. Каких-либо других ограничений на сторону АВ нет, поэтому она может иметь длину 1, 2 или 3.
ответ: 1, 2 или 3
15=5×3
42=7×2×3
105=3×7×5
12) наименьшее кратное "7"
21=7×3
28=7×4
35=7×5