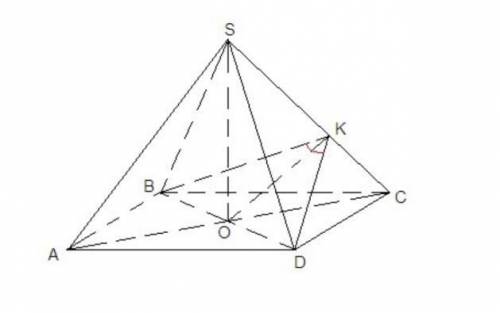
Из задания выходит, что задана правильная четырёхугольная пирамида SАВСД, высота SO которой равна ребру "a". Точка О - центр основания (точка пересечения его диагоналей).
Пусть длина ребра основания а = 1, диагональ основания d = √2.
Для определения угла между смежными боковыми гранями проведём сечение через диагональ ВД основания перпендикулярно боковому ребру . Получим равнобедренный треугольник ВКД, угол К которого равен углу между боковыми гранями.
Высоту из вершины К этого треугольника найдём как высоту h из вершины прямого угла в треугольнике SOД. Для этого найдём длину бокового ребра SД:
SД = √(1² + (√2/2)²) = √(1 + (2/4)) = √(3/2).
h = (1*(√2/2)/√(3/2) = 1/√3.
Теперь можно получить ответ:
угол ВКД = 2arc tg((d/2)/h) = 2arc tg((√2/2)/(1/√3)) = 2arc tg√(3/2) =
= 2*50,76848 = 101,537 градуса.
Пошаговое объяснение:
1) 18,1-5,6=12,5
-11,9+8=-3,9
34,4-12,5=21,9
21,9+(-3,9)=21,9-3,9=18
18-25,
2) =6/7*(2,86-0,64)=6/7*2,22=6/7*111/50=
333/175=1 158/175
3) =-5m
4) =-8k+24+4k-8-6k-2=-10k+14
5) =5/8(18/5a-18/5b)-7/2(4/7a-1/5b)=
9/4a-9/4b-2a+7/10b=2,25a-2,25b-2a+0,7b=0,25a-1,55b