а) 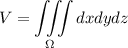 . В нашем случае
. В нашем случае 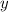 меняется от
меняется от 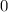 до
до 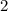 ,
,  меняется от
меняется от 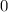 до
до 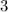 , а
, а  заключен между
заключен между 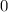 и
и 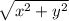 . По сути
. По сути  можно представлять себе как множество отрезков высоты
можно представлять себе как множество отрезков высоты 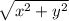 выпущенных из точки
выпущенных из точки 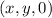 , причем эти точки берутся из прямоугольника
, причем эти точки берутся из прямоугольника ![[0,2]\times [0,3]](/tpl/images/4758/9834/e2d7a.png) .
.
Итак, 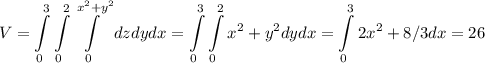 .
.
б) Здесь рассуждения такие же, только  представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости
представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости 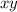 . Величина
. Величина  будет меняться от
будет меняться от 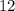 до минимального значения на
до минимального значения на  , что соответствует максимуму
, что соответствует максимуму 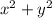 на
на  -- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке
-- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке 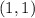 (а начало координат не подходит). Значит,
(а начало координат не подходит). Значит, 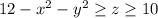 . Итого:
. Итого: 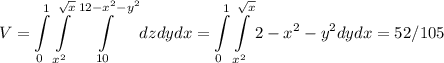 .
.
в) Здесь удобно сделать замену координат: 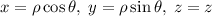 , тогда поверхности:
, тогда поверхности: 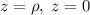 . Якобиан
. Якобиан 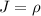 , имеем:
, имеем: 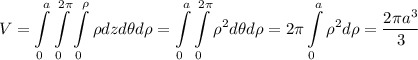 .
.
Всего 8 различных таких троек.
Пошаговое объяснение:
Итак, известно: 3 числа 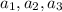 такие, что:
такие, что:
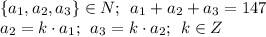
Найти: число возможных вариантов 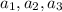
Решение: т.к. все 3 числа - члены геом. прогрессии, запишем так:
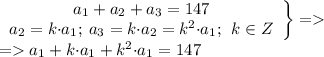
Теперь преобразуем полученное равенство:
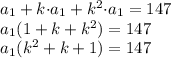
Сделаем замену:
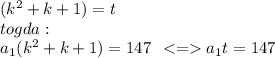
Получили произведение 2 множителей, про которые известно, что а1 - натуральное, k - целое..
т.к. а1 - натуральное, 147 - натуральное =>
=> и значение t тоже должно быть натуральным числом.
И, очевидно, значение а1 и t ограничено сочетаниями множителей, на которые можно разложить 147.
Разложим:
147 = 1•3•7•7
Итак, как а, так и t могут принимать значения из множества: {1; 3; 7; 21; 49; 147}
Рассмотрим t. обратная замена;
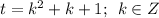
График t(k)= k²+k+1 - парабола, с вершиной в точке 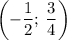 , ветви вверх.
, ветви вверх.
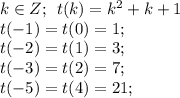
При значениях t = 49; t = 147 k - не является целым числом, так что они для t не подойдут
Итак: Всего возможно 8 различных значений для k
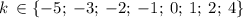
И для каждого варианта k существует единственный вариант значения а1.
То есть - следовательно, всего различных наборов чисел может быть столько же, сколько различных значений k.
Т. е. всего 8 вариантов различных троек чисел