На 40% увеличится площадь прямоугольника, если его длину увеличить на 15%, а ширину увеличить на 22%.
Пошаговое объяснение:
Если его длину увеличить на 15%, а ширину увеличить на 22%, то:
Представим проценты в виде дроби: 0.15 и 0.22, тогда:
Длина a+0.15a = 1.15a; Ширина b+0.22b = 1.22b
S = a*b = 1.15a*1.22b = 1.4ab
Отношение площадей: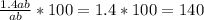 
, отнимаем от значения 100% обычной площади и получаем: 140 - 100 = 40%.
На 40% увеличится площадь прямоугольника, если его длину увеличить на 15%, а ширину увеличить на 22%.
1. Найти уравнение касательной к графику функции f(x)=3x^2−12x+2 в точке x₀=1.
Уравнение касательной к графику функции f(x) в точке x₀=a находится по формуле:
y=f(a)+f′(a)(x−a) (1)
Сначала найдём производную функции f(x):
f′(x)=6x−12
Затем найдём значение функции и её производной в точке a:
f(a)=f(1)=−7
f′(a)=f′(1)=−6
Подставим числа a=1; f(a)=−7; f′(a)=−6 в формулу (1):
y=−7−6(x−1)=−6x−1
ответ: y=−6x−1
2. Найти уравнение касательной к графику функции f(x)=2x^3+2x−1 в точке x₀=1
Решение
Уравнение касательной к графику функции f(x) в точке x₀=a находится по формуле:
y=f(a)+f′(a)(x−a) (1)
Сначала найдём производную функции f(x):
f′(x)=6x^2+2
Затем найдём значение функции и её производной в точке a:
f(a)=f(1)=3
f′(a)=f′(1)=8
Подставим числа a=1; f(a)=3; f′(a)=8 в формулу (1):
y=3+8(x−1)=8x−5
ответ: y=8x−5.
15:0,5=30
24:0,12=200