1) -3
2) 0
3) ∞
Пошаговое объяснение:
Для вычисления предела на бесконечности частного двух многочленов можно сравнить степени многочленов - если степень числителя больше, то предел частного будет равен бесконечности. если степени одинаковые, то предел будет равен отношению коэффициентов при старших степенях. Если степень в значменателе больше, то предел будет равен нулю. Примеры на все три случая:
1) 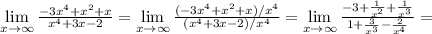
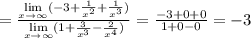
2) 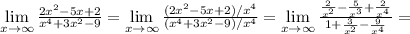
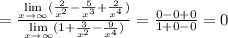
3)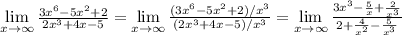
В числителе стоит бесконечно большая функция, знаменатель стремится к 2 (то есть имеет конечный предел), значит частное будет бесконечно большим.
Пошаговое объяснение:
1) f(x) =1/5 x⁵ - 4/3 x² + 125 ;
f'(x) = 1/5 * 5 x⁴ - 4/3 *2x = x ( x³ - 8/3 ) ;
f'(x) = 0 ; x ₁ = 0 ; x³ - 8/3 = 0 ; x ₂ = 2/∛3 ;
f'( - 1 ) > 0 ; f'( 1 ) < 0 ; f'( 10 ) > 0 ;
( - ∞ ; 0 ] i [ 2/∛3 ; + ∞ ) - проміжки зростання функції ;
[ 0 ; 2/∛3 ] - проміжки спадання функції .
х = 0 - точка максимуму функції ; f( 0 ) = 125 .
2) 2sin²x = √2 cos( 3π/2 + x ) , xЄ [π/2 ; 2π ] ;
2sin²x = √2 sinx ;
2sin²x - √2 sinx = 0 ;
sinx (2sinx - √2) = 0 ;
sinx = 0 або 2sinx - √2 = 0 ;
х = πn , nЄ Z ; sinx = √2/2 ;
x= π i х = 2π із даного x = ( - 1 )ⁿ * π/4 + πn , nЄ Z ;
проміжка ; тільки х = 3π/4 належить даному проміжку .
В - дь : 3π/4 , π , 2π .
В = 0,(17)
А больше В