Вкондитерской приготовили торт в форме куба. его разрезали на 4 части. на заливку всего торта шоколадом,кроме основания,ушло 400 г шоколада. сколько необходимо грамм шоколада, что бы залить шоколадом стороны кусочков торта без шоколада? ! а)200г б)300г в)400г г)500г

👇

Ответ:

ник4858

22.08.2021

Пусть ребро куба а. Площадь залитой шоколадом поверхности а*а*5=С.
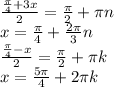
Площади которые нало залить шоколадом (а*а /2)*2*4=а*а*4=С*0,8. На это надо 320 г шоколада.
По -видимому, к этому надо добавит площадь незалитого ранее основания. Для этого следует добавить еще 400:5=80г
Значит всего надо те же 400 г шоколада.

4,8(21 оценок)

Открыть все ответы

Ответ:

wildforme

22.08.2021

В условии задачи не сказано, какое именно количество коротких, средних и длинных было. Но точно, по одной каждого вида, потому что она их резала. Рассмотрим самую "плохую" ситуацию, что было всего по одной средней и длинней, а остальные- короткие. Получается, что из средней у нас есть -15 кусочков, из длинной- 22 кусочка, а из оставшихся 110 коротких ленточек 8*110=880 ленточек. Итого 15+22+880= 917. Очевидно, что это не 2015 ленточек. Получается, что мы не можем сказать, что , однозначно, всех лент хватит на 2015 ленточек

4,5(51 оценок)

Ответ:

konuj

22.08.2021

Я решил так: Домножаем неравенство на √(2)/2.
$\frac{ \sqrt{2} }{2} cosx- \frac{ \sqrt{2} }{2} sinx+cos2x \geq 0 \\ 
cos( \frac{ \pi }{4} )cosx-sin( \frac{ \pi }{4} )sinx+cos2x \geq 0 \\ 
cos( \frac{ \pi }{4}+x)+cos2x \geq 0 \\ 
2cos( \frac{ \frac{ \pi }{4}+3x}{2} )cos( \frac{ \frac{ \pi }{4}-x}{2} ) \geq 0
$
Теперь ищем нули.
$\frac{ \frac{ \pi }{4}+3x}{2} =\frac{ \pi }{2} + \pi n \\ 
x=\frac{ \pi }{4}+ \frac{2 \pi }{3} n \\ 
\frac{ \frac{ \pi }{4}-x}{2}=\frac{ \pi }{2} + \pi k \\ 
x= \frac{5 \pi }{4} +2 \pi k \\ 
$
n∈Z, k∈Z
Теперь нужно применить метод интервалов. С второй серией корней все ясно, просто отмечаем на триг окружности точку 5pi/4. А как быть с первой серией? Сделаем так, отметим ВСЕ точки,которые дает эта серия, на круге. Подставим k=-1, получим -5pi/12 (эта точка лежит между 3pi/2 и 2pi.
При k =0: pi/4
При k=1: 11pi/2 (между pi/2 и 5pi/4). Все, если мы теперь возьмем k=2, то мы опять попадем в точку 19pi/12 находящуюся на круге там же где -5pi/12. Мы замкнули круг.
Теперь подставляем значение x из любого промежутка, находим знак функции на этом интервале, а дальше знаки чередуем.
Получаем как раз указанный тобой ответ.

4,6(95 оценок)

Это интересно:

Стиль-и-уход-за-собой

14.02.2023

Контроль волос африканского стиля: советы и инструкции...

Философия-и-религия

22.11.2020

5 способов, как быть ближе к Аллаху: разбираемся в духовном росте...

Здоровье

29.01.2020

Как похудеть в лице: эффективные способы...

Компьютеры-и-электроника