Question

Бог истины всегда говорит правду, бог лжи — всегда обманывает, бог случая может говорить и правду, и ложь в произвольном порядке. требуется определить богов, задав 3 вопроса, на которые можно ответить «да» или «нет» . каждый вопрос задаётся только одному богу. боги понимают язык, но отвечают на своём языке, в котором есть 2 слова «da» и «ja», причём неизвестно, какое слово обозначает «да» , а какое «нет».

Answer 1

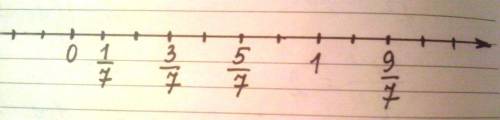
Первым вопросом мы должны найти бога, который не является богом случая, то есть является либо богом правды, либо богом лжи. Есть множество вопросов, которые могут быть заданы для достижения этой цели. Одна из стратегий — использование сложных логических связей в самом вопросе.

Вопрос: "Означает ли «da» «да», только если ты бог правды, а бог B — бог случая?". Другой вариант вопроса: «Является ли нечётным числом количество правдивых утверждений в следующем списке: ты — бог лжи, „ja“ обозначает „да“, B — бог случая?»

Решение задачи может быть упрощено, если использовать условные высказывания, противоречащие фактам . Идея этого решения состоит в том, что на любой вопрос Q, требующий ответа «да» либо «нет», заданный богу правды или богу лжи:

Если я с тебя Q, ты ответишь «ja»?

результат будет «ja», если верный ответ на вопрос Q это «да» и «da», если верный ответ «нет». Для доказательства этого можно рассмотреть восемь возможных вариантов, предложенных :

Предположим, что «ja» обозначает «да», а «da» обозначает «нет»: Мы спрашивали у бога правды, и он ответил «ja». Поскольку он говорит правду и верный ответ на вопрос Q — «ja», оно обозначает «да».

Используя этот факт можно задавать вопросы:

Спросим бога B: «Если я с у тебя „Бог А — бог случая?“, ты ответишь „ja“?». Если бог B отвечает «ja», значит, либо он бог случая (и отвечает случайным образом), либо он не бог случая, а на самом деле бог A — бог случая. В любом варианте, бог C — это не бог случая. Если же B отвечает «da», то либо он бог случая (и отвечает случайным образом), либо B не бог случая, что означает, что бог А — тоже не бог случая. В любом варианте, бог A — это не бог случая. Спросим у бога, который не является богом случая (по результатам предыдущего вопроса, либо A, либо C): «Если я с у тебя: „ты бог правды?“, ты ответишь „ja“?». Поскольку он не бог случая, ответ  «ja» обозначает, что он бог правды, а ответ «da» обозначает, что он бог лжи. Спросим у этого же бога «Если я у тебя с Бог B — бог случая?“, ответишь ли ты „ja“?». Если ответ «ja» — бог B является богом случая, если ответ «da», то бог, с которым ещё не говорили, является богом случая.