1. А) x^2+5x-6<0
Х^2+6X-X-6 < 0
X*(X+6)-(X+6) < 0
(X+6)*(X-1) < 0
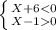
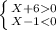
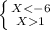
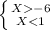
X ∈ ∅
X ∈ (-6,1)
б) 8x^2+24x ≥ 0
8Х*(Х+3) ≥ 0
Х*(Х+3)≥0
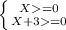
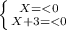
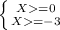
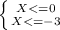
X∈ [0, + ∞)
X∈ ( -∞, -3]
B) x^2>4
|X| > 2
X>2, X≥0
-X>2, X<0
X∈(2, +∞)
X < -2, X < 0
X∈ ( 2, +∞)
X ∈ ( -∞, -2)
г) x^2-12x+36>0
(X-6)^2>0
(X-6)^2=0
X=6
2. 
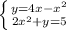
2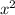
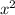+4x - = 5
x= -5
x= 1
y = 4*(-5) - (-5)^2
y = 4*1-1^2
y = -45
y = 3
(
, 
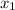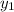) = (-5, -45)
(
, 
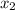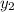) = (1, 3)
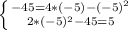
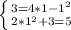
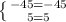
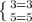
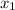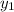(, ) = (-5, -45)
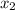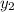( , ) = (1,3)
Привет-привет!
Рассмотрим треугольник ECD. ∠EDA= ∠CED (как накрест лежащие при BC||AD и секущей ED). Из этого следует, что треугольник CED равнобедренный, следовательно, CD=EC=5 см.
Зная, что ABCD - параллелограмм, то по свойству параллелограмма AB=CD=5 см.
Теперь рассмотрим треугольник ABE. ∠EAD=∠BEA(как накрест лежащие при BC||AD и секущей AE), из этого следует, что треугольник ABE — равнобедренный. Тогда AB=BE=5 см.
Заметим, что BC=BE+EC=5+5=10 см. По свойству параллелограмма BC=AD=10 см. Тогда найдем площадь параллелограмма:
P(ABCD)=AB+BC+CD+DA=2BC+2AB=2*10+2*5=20+10=30 см.
ответ: 30 см
