1. V(параллелепипеда)=4*8*16=512 см³
ребро куба а=∛512=8 см.
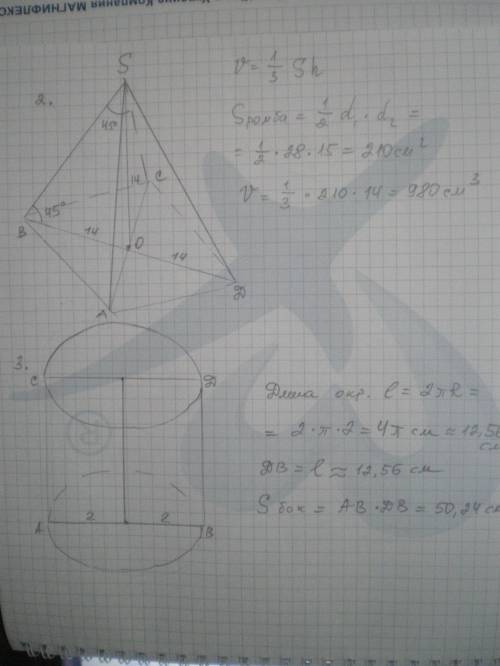
2. Пусть дана пирамида SABCD, SО - высота, АС=15 см, ВD=28 см, ∠SBO=45°. Найти объём пирамиды V.
В основании пирамиды лежит ромб, диагонали ромба в точке пересечения делятся пополам. Значит, ВО=ОД=28:2=14 см.
Рассмотрим Δ SВО - прямоугольный. ∠SBO=45°, значит и ∠ВSB=45°, т.е. ΔSВО - равнобедренный и SВ=SО=14 см.
Найдем площадь основания по формуле
S(ромба)=1\2 * АС * ВD = 1\2 * 28*15 = 210 см²
Найдем объем пирамиды
V=1\3 * S * h = 1\3 * 210 * 14 = 980 cм³.
3. Пусть дан цилиндр, АВ - диаметр, АВ=4 см, ДВ - высота, ДВ=L. Найти S боковой поверхности.
L=2πR=2*3,14*2≈12,56 см.
S боковой поверхности=АВ*ВД=4*12,56=50,24 см²
ответ - 41 плитка
1 шаг сразу определимся, что, поскольку из 11 плиток в ряду не вышло квадрата, то у нас плиток < 12
2 шаг пусть при укладке по 8 плиток, остаток будет а
при укладке по 8 плиток остаток будет b
тогда a-b = 5, т.е. а >5 но из того, что при раскладке по 7 плиток на полный ряд не хватит, мы делаем вывод о том, что а < 7
и вот мы определились с a и b
5 < a < 7 ⇒ a=6 b= 1
3 шаг и теперь нам надо просто найти число < 81, которое при делении на 8 даст остаток (1), а при делении на 8 даст остаток (7)
для 8 с остатком (1) для 7 с остатком (6)
17 20
25 27
33 34
41 41
49 48
57 55
65 62
73 69
и вот у нас совпало только одно число - 41
значит у нас была 41 плитка
41 : 7 = 5(6) 5 рядов по 7 плиток и в 6ом ряду 6 плиток
41 : 8 = 5(1) 5 рядов по 8 плиток и в 6ом ряду 1 плитка
ответ
изначально была 41 плитка