Чтобы перевести бесконечную десятичную дробь в обыкновенную, нужно в числитель поставить период, а в знаменатель число из одних 9, которых должно быть столько же, сколько цифр в периоде.
0,(12) = 12/99 = 4/33
Если перед периодом есть дополнительные цифры, то нужно представить дробь со знаменателем 10, 100 и т.д.
Тогда знаменатель из 9 у основной дроби тоже нужно умножить на 10, 100 и т.д. соответственно.
7,5(4) = 7+5/10+4/90 = (630+45+4)/90 = 679/90 = 7 49/90
1,0(12) = 1+12/990 = 1+4/330 = 334/330
0,(35) = 35/99
Пошаговое объяснение:
; 
Пошаговое объяснение:
Первое условие для того, чтобы это можно было сделать знаменатель должен быть кратен 8 (делиться на 8 без остатка):
65 : 8 = 8 и 1 в остатке. Условие не выполняется.
88 : 8 = 11. Условие выполняется.
9 : 8 = 1 и 1 в остатке. Условие не выполняется.
104 : 8 = 13. Условие выполняется.
24 : 8 = 3. Условие выполняется.
Но к сожалению не во всех из дробей с этим знаменателями числитель делится на второй множитель без остатка:
88 : 8 = 11, при этом 55 : 11 = 5. Подходит. Дробь мы можем представить, как дробь 
.
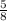104 : 8 = 13, однако 8 не делится на 13 и представить дробь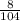 
как дробь с знаменателем 8 мы не можем, так как 
.
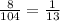104 : 8 = 13, однако 16 не делится на 13 без остатка и представить дробь 
как дробь с знаменателем 8 мы не можем, так как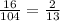 
.
104 : 8 = 13, при этом 13 : 13 = 1. Подходит. Дробь мы можем представить, как дробь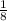 
.
24 : 8 = 3, однако 16 не делится на 3 без остатка и представить дробь 
как дробь с знаменателем 8 мы не можем, так как 
.
x-> -2
ответ ниже |
\/