ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
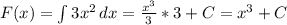
Подставляем в первообразную границы интегрирования:

2.
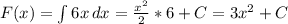
Подставляем в первообразную границы интегрирования:
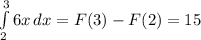
3.

Подставляем в первообразную границы интегрирования:
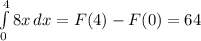
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
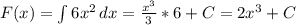
Подставляем в первообразную границы интегрирования:
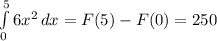
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
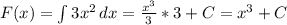
Подставляем в первообразную границы интегрирования:

2.
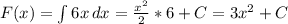
Подставляем в первообразную границы интегрирования:
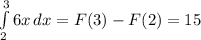
3.

Подставляем в первообразную границы интегрирования:
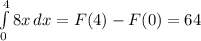
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
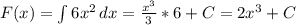
Подставляем в первообразную границы интегрирования:
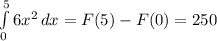
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

Найдите основание трапеции, учитывая, что они относяться как 3 : 4. Пусть одна часть x, сл. верхнее основание 3x, а нижнее - 4x
По формуле трапеции: S = h * ( a + b ) / 2
Где h — высота трапеции, a и b — верхнее и нижнее основания трапеции.
S = 5*(3x+4x)/2 -> S = 35x/2
35 = 35x/2 -> 35x = 2*35 -> x = 2
Нижнее основание: 2*4=8