Пошаговое объяснение:4)f(x)=Sinx, x₀=-π/3; уравнение касательной имеет вид у= f(x₀)+f'(x₀)·(x-x₀). Найдём f(x₀)= Sin (-π/3)=-√3/2 f'(x)=Cosx f'(x₀) =Cos(-π/3)=Cos π/3 = 1/2 Тогда у=-√3/2 + 1/2 ·(х+π/3)=1/2 ·х +π/6 - √3/2;
Отв: у=1/2 ·х +π/6 - √3/2 3)f(x)=(x+2)/(x-4), x₀=3 уравнение касательной имеет вид у= f(x₀)+f'(x₀)·(x-x₀). f(x₀)=(3+2)/3-4)=-5; f'(x) = -6/(х-4)² ⇒ f'(x₀) = -6/(3-4)²=-6 ⇒ у= -5-6·(х-3)=-6х+13 Отв: у=-6х+13 2) f(x)= x²-√x, x₀=4 уравнение касательной имеет вид у= f(x₀)+f'(x₀)·(x-x₀). f(x₀)=4²-√4=16-2=14; f'(x) = 2х - 1/2√х ⇒ f'(x₀) = 2·4 - 1/2√4 = 31/4 ⇒ у= 14 +31/4 ·(х-4)= 7,75х-17 Отв: у=7,75х-17


Вертикальные асимптоты проходят в точках разрыва функции. Их нет.
Горизонтальных асимптот графика функции y=f(x) тоже нет, так как функция вместе с переменной стремится к бесконечности.
Уравнения наклонных асимптот обычно ищут в виде y = kx + b.
По определению асимптоты: lim (kx + b – f(x)) при x →∞.
Находим коэффициент k:
k = lim( f(x)/x) при x →∞.
〖k=lim┬(x→∞)〗〖(3x+2arcctg(x))/x〗=3.
Находим коэффициент b:
b = lim (f(x) – kx) при x →∞.
b = lim (3x + 2arcctg(x) – 3x) при x →∞ = lim (2arcctg(x)) при x →∞ = 0.
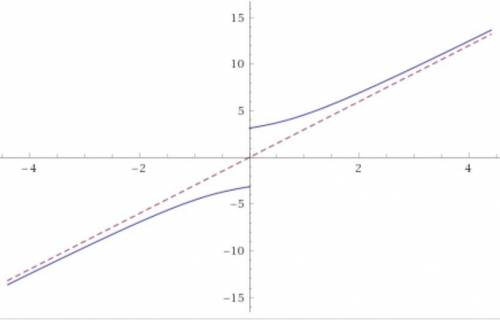
Получаем уравнение наклонной асимптоты: y = 3x .
9b+6b=615+15
15b=630
b=630:15
b=42
Б) 2а+123а+97=472
2а+123а=472-97
125а=375
а=375:125
а=3
В) 17х-х+5х-19=190
17х-х+5х=190+19
21х=209
х=209:21
х~9,9
Г) 73у-у-22у+40=190
73у-у-22у=190-40
50у=150
У=150:50
у=3