33/65
Пошаговое объяснение:
так как sin(a+b)=sin(a)*cos(b)+sin(b)*cos(a),
то sin(a+b)=
так как:
1) sin (a) = 3/5 (по условию)
2) cos(b) = -5/13 (по условию)
отметим, что так как а принадлежит 2-ой координатной четверти на графике, то sin(a)>0, cos(a)<0, но b принадлежит 3-ей координатной четверти, поэтому sin(b)<0, cos(b)<0
при этом sin(х) ^2 + cos (х) ^2=1
поэтому:
3) sin(b) ^2 + (-5/13)^2=1
sin(b) ^2+25/169 = 1
sin(b) ^2 = 1 - 25/169
sin(b) ^2 = 144/169 = (12/13)=(-12/13), при этом sin(b)<0
следовательно sin(b) = -12/13
4) cos(a) ^2 + (3/5)^2 = 1
cos(a) ^2 + 9/25 =1
cos(a) ^2 = 1 - 9/25
cos(a) ^2 = 16/25 = (4/5)^2 = (-4/5)^2, при этом cos(a)<0
следовательно cos(a) = -4/5
5) sin(a)*cos(b)+sin(b)*cos(a) =
= (3/5) * (-5/13) + (-12/13) * (-4/5) = -15/65 + 48/65 = (48-15)/65 = 33/65
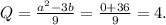
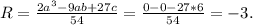
{x²+y²=13
4х=(26-ky)|÷4
x=(26-ky)/4
((26-ky)/4)²+y²=13
((26-ky)²/16)+y²=13|×16
(26-ky)²+16y²=208
26²-2×26×ky+k²y²+16y²=208
676-52ky+k²y²+16y²-208=0
k²y²+16y²-52ky+468=0
(k²+16)y²-52ky+468=0
Квадратное уравнение имеет один корень, когда дескрименант равен нулю.
b²-4ac=D
a=(k²+16)
b=(-52k)
c=468
D=0
(-52k)²-4×(k²+16)×468=0
2704k²-1872×(k²+16)=0
2704k²-1872k²-29952=0
832k²-29952=0
832k²=29952|÷832
k²=36
k1=6 - является решением, так как в условии спрашивается при каком положительном значении k.
k2=(-6).
Проверка:
{4x+ky=26
{x²+y²=13
{4x+6у=26
{x²+y²=13
4х=(26-6y)|÷4
x=(26-6y)/4
х=(26/4)-(6у/4)
х=(6,5-1,5у)
х²+y²=13
(6,5-1,5у)²+у²=13
6,5²-2×6,5×1,5у+(-1,5у)²+у²-13=0
42,25-19,5y+2,25у²+у²-13=0
3,25у²-19,5у+29,25=0
D²=(-19,5)²-4×3,25×29,25
D²=380,25-380,25
D²=0
D=0 => y=(-b)/2×a
y=(-(-19,5))/2×3,25
y=(19,5/6,5)
y=3
х=(6,5-1,5у)
x=(6,5-1,5×3)
x=(6,5-4,5)
x=2
{4x+6у=26
{x²+y²=13
4×2+6×3=26
8+18=26
26=26-истина
2²+3²=13
4+9=13
13=13-истина.
ответ: При k=6, система уравнений имеет единственное решение (2;3).