исследуем функцию f(x)=x²-4|x|-a+3 на чётность:
1) она не прерывна на области определения, то есть
D(f)=(-∞;+∞)
2) f(-x)=(-x)²-4|-x|-a+3=x²-4|x|-a+3=f(x)
f(-x)=f(x) ⇒ функция чётная
№224
График четной функции симметричен, относительно оси у.
Значит она имеет равное количество положительных и отрицательных действительных корней (если они вообще есть).
Поэтому 2 положительных и 1 отрицательный корень она иметь не может.
ответ: А)∅
№225
Как уже было сказано: такая функция имеет равное количество положительных и отрицательных действительных корней, причем - это противоположные числа (x=±x₀). А сумма противоположных чисел равна нулю
Так как это тест, можно сразу давать ответ
ответ: С)0.
Но если нужно полное решение, то надо еще убедится, что при а≥3 корни вообще есть!
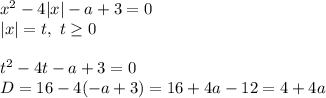
квадратное уравнение имеет корни при D≥0
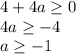
корни полученного квадратного уравнения:
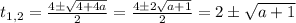
так как t=2+√(a+1) >0, то исходное уравнение будет иметь как минимум 2 корня (|x|=t ⇒ x=±t) при а≥-1.
Значит при а≥3 уравнение тем более будет иметь корни, а их сумма равняться нулю
x-y=104
если решать системой
избавимся от x
2y=3574
y=3574:2
y=1787
подставляем в любое из уравнений (я сделаю в 1)
x+1787=3678
x=3678-1787
x=1891
проверка
1891+1787=3678
1891-1787=104