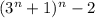 делится на
делится на 
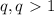 :
: 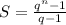 ;
;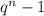 делится на
делится на  . Пусть здесь
. Пусть здесь 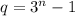 . Имеем:
. Имеем: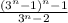 число целое (*). Нам же нужно доказать, что число
число целое (*). Нам же нужно доказать, что число 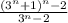 целое.
целое. дает остаток 1 от деления на число
дает остаток 1 от деления на число  ; Осталось лишь найти остаток от деления на то же число числа
; Осталось лишь найти остаток от деления на то же число числа 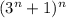 . Найдем произведение этих двух чисел:
. Найдем произведение этих двух чисел: 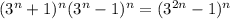 Пусть остаток от деления этого числа на число
Пусть остаток от деления этого числа на число  равен x; Мы знаем, что остаток от деления числа
равен x; Мы знаем, что остаток от деления числа 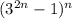 на число
на число 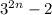 равен 1. А остаток от деления числа
равен 1. А остаток от деления числа 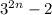 на число
на число  равен 2. Стало быть, остаток от деления числа
равен 2. Стало быть, остаток от деления числа 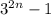 на число
на число  равен 3.
равен 3.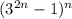 на число
на число  равен
равен 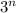 ; Но
; Но 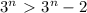 , поэтому остаток равен 2. Мы только что нашли x. x = 2, а остаток от деления на число
, поэтому остаток равен 2. Мы только что нашли x. x = 2, а остаток от деления на число  числа
числа  , как уже говорилось равен 1. Значит искомый остаток от деления на
, как уже говорилось равен 1. Значит искомый остаток от деления на  числа
числа 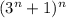 равен 2. Отсюда и следует, что
равен 2. Отсюда и следует, что 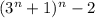 делится на
делится на 
Полководец Великой Отечественной войны. Маршал Советского Союза.
Георгий Константинович Жуков родился в калужской деревне Стрелковка (ныне Жуково) в простой крестьянской семье. Службу в русской армии начал в 1915 году. Участвовал в Первой мировой войне, дослужился до унтер-офицера, награжден двумя Георгиевскими крестами.
В Гражданскую войну стал добровольцем, вступил в Красную армию. Вскоре решительный и храбрый кавалерист из рядового стал командиром взвода, а затем и кавалерийского эскадрона. Боевой путь Жукова в годы Гражданской войны отмечен участием в боях на Восточном, Западном и Южном фронтах. Участвовал он и в ликвидации послевоенного бандитизма, мешавшего налаживанию мирной жизни в стране.
Высшего военного образования Жуков не получил. За его спиной были лишь кавалерийские курсы (1920 год), курсы усовершенствования командного состава кавалерии (1925 год) и курсы усовершенствования высшего начальствующего состава (1930). Академическое образование Жукову заменяли опыт Гражданской войны и последующая служба на различных должностях в Красной армии, а самое главное — природное дарование.
После Гражданской войны, когда армия была сокращена в несколько раз до штатов мирного времени, Жуков остался в ее рядах в той же должности командира кавалерийского эскадрона. Уже в июле 1923 года стал командиром полка красной кавалерии. Через семь лет — командиром кавалерийской бригады.
В начале 1931 года комбриг Г.К. Жуков назначается на должность инспектора кавалерии Красной армии. Вскоре он становится командиром 4-й кавалерийской дивизии. С 1937 года — командир 3-го кавалерийского корпуса, с 1938 года — командир 6-го кавалерийского корпуса РККА. В июле 1938 года Жуков назначается заместителем командующего войсками Белорусского военного округа. Его счастливо обошли сталинские репрессии в армии и на флоте, когда многие красные командиры горнило Гражданской войны, ушли в небытие или оказались в бериевских концлагерях.
В июле 1939 года Жуков был назначен командующим 1-й армейской группой советских войск в Монголии. К тому времени обстановка на Дальнем Востоке была тревожной — японская армия, оккупировавшая Маньчжурию, встала против советских границ. Военное столкновение было невозможно предотвратить. Проба сил перед еще далеким 1945 годом состоялась у озера Хасан и на реке Халхин-Гол.
Армейская группа Жукова совместно с армией Монгольской Народной Республики успешно провели наступательную операцию — окружили и полностью разгромили крупную группировку японских войск на реке Халхин-Гол.
Х - это сколько лет дочери
Тогда возраст матери - 4х лет и 24+х
4х=24+х
4х-х=24
3х=24
х=8
ответ: 8 лет.