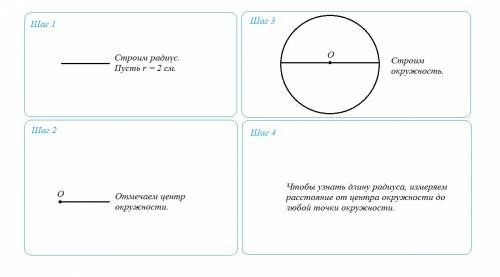
1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.
Всего 720 расстановок
Пошаговое объяснение:
если расстанавливать книги по истории отдельно то всего расстановок только по истории 3!=1*2*3=6
если расстанавливать книги по алгебре отдельно то всего расстановок только по алгебре 4!=1*2*3*4=24
а у нас ещё 4 книги по алгебре и между каждой книгой и по бокам будет 5 мест где в каждом месте по 3 истории в разных расстановках
как показано ниже:
ист. ист. ист. алг. алг. алг. алг.
алг. алг. алг. алг. ист. ист. ист.
алг. алг. алг. ист. ист. ист. алг.
алг. алг. ист. ист. ист. алг. алг.
алг. ист. ист. ист. алг. алг. алг.
при это у нас алгебра тоже меняется местами
значит всего расстановок 4!*3!*5=24*6*5=720
S=(7+10)/2*4=34