
Пошаговое объяснение:
Введем замену  ;
;  .
.
Уравнение примет вид

Далее заметим, что для любого  верно
верно  . То есть верхнее ограничение
. То есть верхнее ограничение  выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения 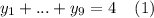 в целых неотрицательных числах.
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов

Розкладемо число 2016 на прості множники
2016=2·2·2·2·2·3·3·7
Розглянемо деякі можливі варанти:
2016=3·3·32·7. Тоді маємо числа -3; -3; -32; -7; 1/224
2016=4·4·6·21. Тоді маємо числа: -4; -4; -6; -21; 1/126
Нам потрібно знайти найбільше п'яте число. Із двох наведених варіантів зрозуміло, що п'яте число буде найбільшим, якщо третє і четверте число будуть найменшими.
2016=12·12·2·7. Тоді маємо числа -12; -12; -2; -7; 1/14.
За умовою треба знайти тільки п'яте число (найбільше), тому відповідь: 1/14