Відповідь:
Наибольшее значение n = 6.
Покрокове пояснення:
1 шаг.) В результате последней операции на прямой оказалось 193 точки. Поскольку Петя ставил новые точки между существующими, значит он поставил:
( 193 - 1 ) / 2 = 96 точек.
На линии до последней операции было:
( 193 - 1 ) / 2 + 1 = 97 точек.
Или
96 + 1 = 97 точек.
2 шаг.) Поставил:
( 97 - 1 ) / 2 = 48 точек.
Было:
48 + 1 = 49 точек.
3 шаг.) Поставил:
( 49 - 1 ) / 2 = 24 точки.
Было:
24 + 1 = 25 точек.
4 шаг.) Поставил:
( 25 - 1 ) / 2 = 12 точек.
Было:
12 + 1 = 13 точек.
5 шаг.) Поставил:
( 13 - 1 ) / 2 = 6 точек.
Было:
6 + 1 = 7 точек.
6 шаг.) Поставил:
( 7 - 1 ) / 2 = 3 точки.
Было:
3 + 1 = 4 точки.
Дальше действия невозможны. Нельзя по предложенной методике удвоения поставить точки, так что-бы в результате получилось 4 точки. В начале на линии было 4 точки. Петя ставил точки по предложенной методике и получил на линии 193 точки за 6 шагов.
ответ: 200 км.
Пошаговое объяснение:
Весь путь разделён на 3 части: 8/20, 7/20 и 50 км. То есть, кроме 50 км, у нас есть ещё
пути.
Весь путь равен 20/20 (=1; мы поделили его на 20 частей, взяли все эти части и получился весь путь). Тогда 50 км составляют
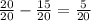
50 км =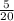 
пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
10 км = 
пути.
Одна двадцатая часть — 10 км. Семь двадцатых частей в семь раз больше, чем одна двадцатая часть:
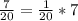
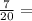10 км * 7 = 70 км.
Восемь двадцатых частей в восемь раз больше, чем одна двадцатая часть:
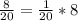
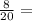10 км * 8 = 80 км.
Обозначим весь путь за s. Тогда
s=I часть + II часть + III часть
s = 80 км + 70 км + 50 км = 200 км.
ответ: 200 км.
