1.а) 9a² - 16=(3а-4)(3а+4)
б) 4y² - 25=(2у+5)(2у+5)
в) x⁴ - 81=(х²-9)(х²+9)=(х-3)(х+3)(х²+9)
г) x³ - 8=(х-3)(х²+3х+9)
д) y³ + 125=(у+5)(у²-5у+25)
е) y² - 26y + 169 =(у-13)²
2. а) 45b + 6a - 3ab - 90= (45b-3ab)+( 6а- 90)=3b(15-а)-6*(15-а)=
3*(15-а)((15-а)(b-2)
б) - 5xy - 40y - 15x - 120=-5*(xy+8y+3x+24)=-5(у*(х+8)+3*(х+8))=-5*(х+8)(у+3)
в) ac⁴- c⁴+ ac³ - c³ =с³(ас-с+а-1)=с³*(а-1)*с+(а-1))=с³*(а-1)*(с+1)
3. а) 4a⁴ - 25b⁴=(2а²-5b²)(2a²+5b²)=(√2a-√5b)(√2a+√5b)(2a²+5b²)
б) b⁶+ 1=(b²)³+1³=(b²+1)*(b⁴-b²+1)
b) m⁴ - 12m² + 36=(m²-6)²=(m-√6)²*(m+√6)²
Пусть скорость мотоциклиста из пункта А до В равна х км/ч
весь путь вычисляется по формуле
S=vt
Тогда время в часах затраченное мотоциклистом от А до В равно
t = S/x
а время от В до А равно
S/2÷ (x+9)+S/2÷30
так как время обратного пути мотоциклиста равно первоначальному, то получаем следующее уравнение
S/x = S/2÷ (x+9)+S/2÷30
Делим обе части уравнения на S, т.к. знаем, что S, не равно 0
переносим в одну сторону. Получаем следующее уравнение
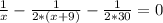
приведем к общему знаменателю
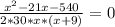
Дискриминант равен (-21)²-4*1* (-540)= 2601
Д больше 0, значит уравнение имеет 2 корня

Так как скорость не может быть отрицательным числом, значит
ответ 36 км/ч
(Log7)x=(log7)54÷3
(Log7)x=(log7)18
X=18
sqrt-корень