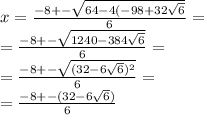
Позначимо всі значення чисел, які обмежують значення з
1. 7,92 < c < 11,1 .
7--7,92--8з---11---11,1. Дивлячись на схематичне розташування числа с, виходячи з даного нерівності, крайні значення число с приймати не може, так як в знаку нерівності немає значення "або дорівнює". Залишається, що с може приймати такі цілі (натуральні) числа: 8; 9; 10; 11. Це відповідь: з = (8; 9; 10;11.
2. 9 < c < 14,5 аналогічно розташуємо задані числа і виберемо всі цілі значення правіше лівого значення, і лівіше правого.
9--10---с - - - 14--14,5. з = (10; 11; 12; 13; 14).
Перенесём правую часть уравнения в левую часть уравнения со знаком минус:
3x^2+8x+19-[3(4-√6)^2 + 8(4-√6)+19] = 0
Раскроем выражение в уравнении:
3x^2+8x+19-3(4-√6)^2 – 8√6+32-19 = 0
Получаем квадратное уравнение:
3x^2+8x-98+32√6 = 0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить с дискриминанта.
Корни квадратного уравнения:
Х1=(√D-b)/2a
X2=(-√D-b)/2a
где D = b^2 - 4*a*c - это дискриминант.
a = 3
b = 8
c = -98 + 32√6
то D = b^2 - 4 * a * c = (8)^2 - 4 * (3) * (-98 + 32*√6) = 1240 - 384*√6
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + √D)/(2*a)
x2 = (-b - √D)/(2*a)
ИЛИ
x1 = -4/3 + 1/6(√общ-384√6) + 1240
x2 = -1/6(√общ-384√6) + 1240 – 4/3