решение слау методом гаусса
решение слау методом гаусса.
запишем систему в виде расширенной матрицы:
1 -2 -1|3
2 1 -3|0
3 3 -6|1
умножим 1-ю строку на (2). умножим 2-ю строку на (-1). добавим 2-ю строку к 1-й:
0 -5 1|6
2 1 -3|0
3 3 -6|1
умножим 2-ю строку на (3). умножим 3-ю строку на (-2). добавим 3-ю строку к 2-й:
0 -5 1 | 6
0 -3 3 | -2
3 3 -6 | 1
умножим 1-ю строку на (3). умножим 2-ю строку на (-5). добавим 2-ю строку к 1-й:
0 0 -12|28
0 -3 3|-2
3 3 -6|1
теперь исходную систему можно записать так:
x3 = 28/(-12)
x2 = [-2 - (3x3)]/(-3)
x1 = [1 - (3x2 - 6x3)]/3
из 1-й строки выражаем x3
x3=28/-12=-2.33
из 2-й строки выражаем x2
x2=)-2-3(-2.33)) /-3= 5/-3=-1.67
из 3-й строки выражаем x1
x1=(1-3(-1.67)-(-6)(-2.33))/3=-8/3=2.67
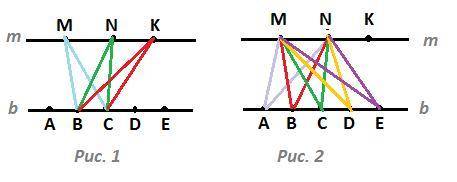
Для построения треугольника нужно взять 3 точки. Эти точки не могут лежать на одной прямой. Чтобы построить треугольник, нужно брать две точки на одной прямой и одну точку на другой.
Рис. 1. На прямой b отмечено 5 точек. Первую точку можно выбрать вторую точку можно выбрать из 4 оставшихся. Так как для треугольника не важно, в каком порядке выбраны вершины, пары точек А,В и В,А равнозначны. Тогда всего вариантов выбрать 2 точки из 5
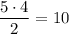
Либо по формуле сочетаний 2 из 5
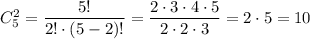
Для каждой пары точек на прямой b, например, для пары В,С, можно выбрать одну из трёх точек, отмеченных на прямой m. Получится 3 треугольника : ΔBCM, ΔBCN, ΔBCK.
Всего треугольников из 2 точек на прямой b и одной точки на прямой m можно построить 10 · 3 = 30.
Рис. 2. На прямой m отмечено 3 точки. Выбрать две из них можно тремя или M,K или N,K. Для каждой пары можно подобрать одну из пяти точек, отмеченных на прямой b. На рисунке показаны треугольники для пары точек M,N.
Всего треугольников из двух точек на прямой m и одной точки на прямой b можно построить 3 · 5 = 15.
30 + 15 = 45
ответ : 45 треугольников
26×2=52
36×2=72
46×2=92
56×2=112
66×2=132
76×2=152
86×2=172
96×2=192
заранее