lg 2x < lg (x+1)
ОДЗ:
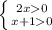
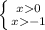
x∈(0;+∞)
lg 2x < lg (x+1)
2x < x + 1
x < 1
С учетом ОДЗ:
x∈(0;1)
ответ: x∈(0;1)
№ 2log2(1-x) < 1
ОДЗ:
1-x>0
x<1
x∈(-∞;1)
log2(1-x) < 1
log2(1-x) < log2(2)
1-x<2
x>-1
С учетом ОДЗ:
x∈(-1;1)
ответ: x∈(-1;1)
№ 3(log3(x) - 2)*sqrt(x^2-4)<=0
ОДЗ:
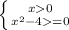
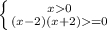
x∈[2;+∞)
(log3(x) - 2)*sqrt(x^2-4)<=0
Т.к. sqrt(x^2-4) - всегда >= 0, то выражение будет < нуля в случае, когда log3(x) - 2 < 0 => Равносилен переход к совокупности:
log3(x) - 2 <= 0 или sqrt(x^2-4)=0
log3(x) <= 2 или (x-2)(x+2)=0
log3(x) <= log3(3^2) или x = ± 2
x <= 9 или x = ± 2
С учетом ОДЗ:
x∈[2;9]
ответ: x∈[2;9]
по озеру 10км х км/ч 10/х ч.
против теч. 4км (х - 3)км/ч 4/(х - 3) ч
V теч = 3 км/ч
V собств. = х км/ч
10/х + 4/(х - 3) = 1 | * х(х-3)
10(х -3) + 4х = х(х -3)
10х -30 +4х = х² -3х
х²-17х +30 = 0
по т. Виета корни 15 и 2(не подходит по условию задачи)
ответ: Vсобств. = 15км/ч
2) S V t
по теч. 15км ( х + 4)км/ч 15/(х +4) ч
по озеру 4км х км/ч 4/х ч.
V собств.= х км/ч
V теч. = 4 км/ч
15/(х +4) + 4/х = 1 | * x(x +4)
15x +4(x +4) = x(x +4)
15x +4x +16 = x² +4x
x² -15x -16 = 0
По т. Виета корни 16 и -1(не подходит по условию задачи)
ответ: V собств. = 16км/ч