104.
1) 37*218+63*218 = 218*(37+63) = 218*100 = 21800
2) 568*43-566*43 = 43*(568-566) = 53*2 = 106
3) 417*187+417*213 = 417*(187+213) = 417*400 = 166800
4) 52*187-52*43-52*44 = 52*(187-43-44) = 52*100 = 5200
105.
1) 359*a+641*17 при a=17
359*17+641*17 = 17*(359+641) = 17*1000 = 17000
2) 769*87-87b при b=369
769*87-87*369 = 87*(769-369) = 87*400 = 34800
106.
1) 5x+7x = 12x
2) 17a-9a = 8a
3) 34a-a = 33a
4) c+72c = 73c
5) 7x+8x+12c = 15x+12c
6) 53y+18y-24y = 47y
7) 14m+15m+16 = 29m+16
8) 69n-n-18 = 68n-18
9) 25x+37x-17x-x = 44x
107.
1) 37a+83a = 120a при а=8
120*8 = 960
2) 82b-28b = 54b при b=32
54*32 = 1728
3) 33c-6c-7c = 20c при c=549
20*549 = 10980
4) 17x-8x+23x-18 = 32x-18 при x=312
32*312-18 = 9966
108.
1) 2491:53 = 47
2) 5698:14 = 407
3) 9792:32 = 306
4) 23655:57 = 415
y = -x-6
Пошаговое объяснение:
Касательная является параллельной другой прямой, если углы их наклона совпадают.
Если Вам известно понятие производной функции в точке, то можно использовать её геометрический смысл: производная в точке равна тангенсу угла наклона касательной в данной точке.
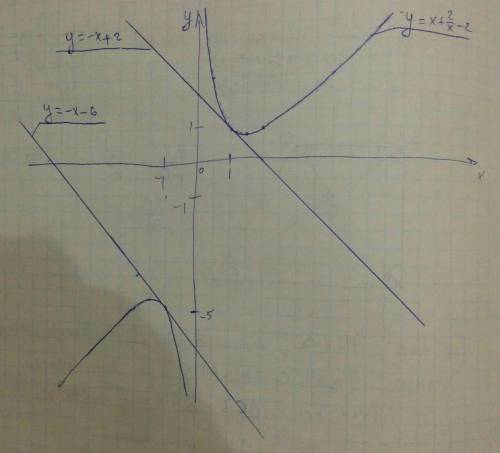
Так, например, наклон функции y=-x+2 одинаков во всех точках и равен -1, т.е. y' = -1.
Необходимо найти такие точки, принадлежащие y=x+2/x-2, в которых производная этой функции была бы равна -1.
Найдём производную: y' = 1 - 2/x^2.
Приравняем производную к -1: 1 - 2/x^2 = -1;
Отсюда следует, что x = ±1 -- это абсциссы точек, в которых производная функции равна -1.
Значения y для этих точек 1 и -5, т.е. точки (1, 1) и (-1, -5).
Касательной к графику функции y = x+2/x-2 в точке (1, 1) является прямая y = -x + 2, которая задана в условии. В точке (-1, -5) касательной является прямая y = -x - 6.
Если Вам неизвестно понятие производной, то просто постройте график данных функций и найдите экспериментально линейкой ту точку, в которой касательная будет параллельна y = -x + 2.
Построение в приложении.
b2 = b1*q; b8 = b1*q^7; b6 = b1*q^5; b4 = b1*q^3
{ b1*q + b1*q^7 = b1*q*(1 + q^6) = 325/128
{ b1*q + b1*q^5 - 65/32 = b1*q*(1 + q^4) - 65/32 = b1*q^3
Перепишем 2 уравнение
{ b1*q*(1 + q^6) = 325/128
{ b1*q*(1 - q^2 + q^4) = 65/32
1 + q^6 раскладываем как сумму кубов
1 + q^6 = (1 + q^2)(1 - q^2 + q^4)
Получаем
{ b1*q*(1 + q^2)(1 - q^2 + q^4) = 325/128
{ b1*q*(1 - q^2 + q^4) = 65/32
Делим 1 уравнение на 2 уравнение
1 + q^2 = (325/128):(65/32) = 325/128*32/65 = 325/65*32/128 = 5/4
q^2 = 5/4 - 1 = 1/4
q = √(1/4) = 1/2 (мы берем 1/2, а не -1/2, потому что прогрессия убывает)
Теперь подставляем
b1*1/2*(1 - 1/4 + 1/16) = 65/32
Умножаем на 2
b1*(16-4+1)/16 = 65/16
Умножаем на 16
b1*13 = 65
b1 = 65/13 = 5
ответ: b1 = 5; q = 1/2