Наличие искомых клеток возможно только при соприкасающихся прямоугольниках.
Наличие искомых клеток возможно только при соприкасающихся прямоугольниках. Предположим, что мы имеем не соприкасающиеся прямоугольника, значит вокруг каждого прямоугольника мы имеем как минимум 3 пустых клетки. Следовательно, общая площадь доски должна быть: 85 клеток, что противоречит условию, т.к. размер поля 8*8=64. Следовательно обязательно имеются смежные прямоугольники, т.е. найдутся 2 клетки, имеющие общую сторону, лежащие в каждом из этих прямоугольников.
Здравствуйте!
Есть такие примеры!
6853...9
+ 2...4...3...
_________
...90257
Смотрим с конца. 9+х=7. Получаем отрицательное число. Такое невозможно. Значит мы должны прибавить десять к 7. 17. 9+х=17; х=8.
Ставим 8, но не забывает прибавить 1 к десяткам, который мы сделали.
6853...9
+ 2...4...38
_________
...90257
1+х+3=5; 4+х=5; х=1.
685319
+ 2...4...38
_________
...90257
3+х=2; отриц. число, прибавляем десяток; 3+х=12; х=9
685319
+ 2..4938
______
..90257
5+4+1=10, т.е. на след. десяток ещё 1 прибавляем.
685319
+ 2..4938
______
..90257
1+8+х=9; х=0
685319
+ 204938
______
..90257
6+2=х; х=8.
685319
+ 204938
______
890257
Сверяем. При сложении получаем сумму, которая нужна.
В вычитании всё тоже самое.
803...0
- 1253...
_______
6...764
0-х=4, отрицательное число, значит нужно прибавить десяток, а из "соседнего левого вычитания" вычесть 1. 10-х=4; х=6.
803...0
- 12536
_______
6...764
х-3-1=6; х-4=6; х=10, но занимаем из левого вычитания 1.
80300
- 12536
_______
6...764
2 (3-1) -5 не равно 7. Значит 12-5=7, занимаем
80300
- 12536
_______
6...764
0-1-2 получится отрицательное число. Значит занимаем. 10-1-2= 7
80300
- 12536
_______
67764
Проверяем. Всё сходится!
В итоге получаем примеры:

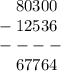
20х+5у-2х+2у=18х+7у