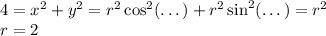

Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
amen2996
amen2996
10.05.2015
Геометрия
10 - 11 классы
ответ дан • проверенный экспертом
Стороны основания правильной четырехугольной пирамиды равны 6,боковые ребра равны 5.Найдите площадь поверхности этой пирамиды
ответ 84 но как?
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ, проверенный экспертом
4.4/5
27
KuOV
главный мозг
5.1 тыс. ответов
47.1 млн пользователей, получивших
Пирамида правильная, значит в основании лежит квадрат, а боковые грани - равные равнобедренные треугольники.
Sпов = Sосн + Sбок
Sосн = а² = 6² = 36 (а - сторона квадрата)
Боковая поверхность - 4 одинаковых равнобедренных треугольника со сторонами 5, 5 и 6. Можно найти площадь одного треугольника по формуле Герона.
Полупериметр: p = (5 + 5 + 6)/2 = 8
Ssad = √(p(p - a)(p- b)(p - c))
Ssad = √(8 · 3 · 3 · 2) = 3 · 4 = 12
Sбок = 4 · Ssad = 4 · 12 = 48
Sпов = 36 + 48 = 84
Площадь боковой поверхности правильной пирамиды можно найти также по формуле:
Sбок = 1/2 Pосн · h, где h - апофема (высота боковой грани), которую можно найти по теореме Пифагора.
а) y'=3x²+2x-5
решаем уравнение 3x²+2x-5=0, получаем x=1 или x =-1 2/3. x(max)=-1 2/3, a x(min)=1. функция возрастает на промежутке (-∞;-1 2/3] и[1;∞), функция убывает на промежутке [-1 2/3; 1].
б) Находим значение функции в точках экстремума если они принадлежат промежутку
y(1)=1+1-5-3=-6
И находим в крайних точках отрезка
y(0)=-3
y(4)=64+16-20-3=57
y(наиб)=57
y(наим)=-6