Пошаговое объяснение:
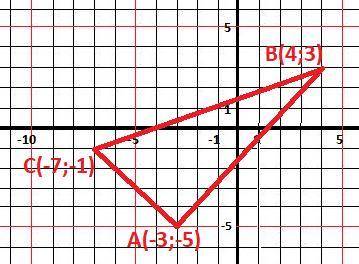
ДАНО: А(-3;-5), В(4;3)
НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(-5-(3))/(-3-(4))=1 1/7 - коэффициент наклона 2) b=Аy-k*Аx=-5-(1 1/7)*(-33) =-1 4/7- сдвиг по оси ОУ
Уравнение Y(АВ) = 1 1/7 *x -1 4/7 - ответ
ДАНО: А(-3;-5), С(-7;-1)
1) k = ΔY/ΔX = (Аy-Сy)/(Аx-Сx)=(-5-(-1))/(-3-(-7))= -1 - коэффициент наклона.
2) b=Аy-k*Аx=-5 - (-1)*(-3) = -8 - сдвиг по оси ОУ
Уравнение Y(АС) = -x - 8 - ответ
ДАНО: В(4;3), С(-7;-1)
1) k = ΔY/ΔX = (Вy-Сy)/(Вx-Сx)=(3-(-1))/(4-(-7))=0,36 - коэффициент наклона.
2) b=Вy-k*Вx=3-(0,36)*4=1,56- сдвиг по оси ОУ
Уравнение Y(ВС) = 0,36*x + 1,56 - ответ.
Рисунок к задаче дополнительно.
ДАНО:Y(x) = x³ -12*x
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Вертикальная асимптота - нет - нет разрывов.
3. Наклонная асимптота - y = k*x+b.
k = lim(+∞) Y(x)/x = +∞ - нет наклонной (горизонтальной) асимптоты.
4. Периода - нет - не тригонометрическая функция.
5. Пересечение с осью OХ.
Разложим многочлен на множители.
Y=x*(x²-12) = x*(x - 2√3)*(x + 2√3) = 0.
Нули функции: Х₁ = -2√3, Х₂ = 0 , Х₃ = 2√3 (≈ +/- 3.46)
6. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;-2√3]U[0;2√3]
Положительная -Y(x)>0 X∈[-2√3;0]U[2√3;+∞)
7. Пересечение с осью OY. Y(0) = 0
8. Исследование на чётность.
В полиноме только нечётные степени - функция нечётная.
9. Первая производная. Y'(x) = 3*x² -12 = 3*(x-2)*(х+2) = 0
Корни Y'(x)=0. Х = - 2, Х= +2.
10. Локальные экстремумы.
Максимум - Ymax(2) = 16. Минимум - Ymin(-2) = -16.
11. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;-2;]U[2;+∞) , убывает - Х∈[-2;2]
12. Вторая производная - Y"(x) = 6* x = 0
Корень производной - точка перегиба Х₆= 0
13. Выпуклая “горка» Х∈(-∞; Х₆ = 0]
Вогнутая – «ложка» Х∈[Х₆ = 0; +∞).
14. График в приложении.
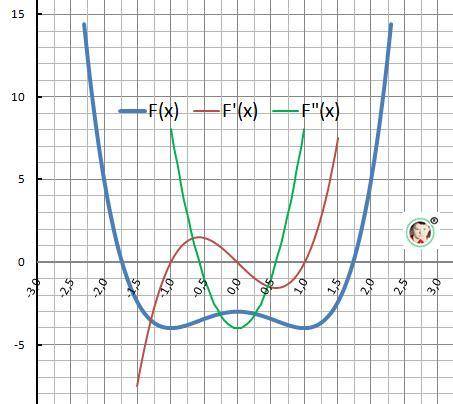
Дано: y(x) = x⁴ - 2*x² - 3
Исследование.
1. Область определения: D(y)= X∈(-∞;+∞).
Гладкая, непрерывная.
2. Вертикальных асимптот - нет.
3. Наклонная асимптота: k = lim(+∞)Y(x)/x = ∞ - асимптот - нет.
4. Нули функции, пересечение с осью ОХ.
Делаем замену переменной: z = x².
z² -2*z - 3 = 0. D=16, z₁ = 3, z₂ = -1
Возвращаемся к подстановке.
x² = 3, x₁ = -√3, x₂ = √3 - нули функции.
х² = - 1 - решения нет
Пересечение с осью ОУ: y(0) = -3.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈[-√3;√3] - между нулями функции.
Положительна: Y>0 - X∈(-∞;-√3]∪[√3;+∞) -вне нулей.
6. Проверка на чётность.
В полиноме функции только четные степени - x⁴, x², x⁰ - функция чётная.
7. Поиск экстремумов по первой производной.
y'(x) = 4*x³ -4*x = 4*x*(x²-1)= 4*x*(x-1)*(x+1) 0.
Точка экстремумов: x₁ = -1, x₂ = 0, x₃ = 1.
8. Локальные экстремумы.
Максимум: y(0) = -3.
Минимумы: y(-1) = y(1) = - 4.
9. Интервалы монотонности.
Возрастает - X∈[-1;0]∪[1;+∞).
Убывает: X∈(-∞;-1]∪[0;1].
10. Поиск перегибов по второй производной.
y"(x) = 12*x² - 4 = 0. x² = 1/3.
Корни уравнения: x₁ = - √3/3. x₂ = √3/3 (≈0.57)
11. Вогнутая - "ложка"- X∈(-∞;-√3/3]∪[√3/3;+∞).
Выпуклая - "горка" - Х∈[-√3/3;√3/3]
12. Область значений. E(y) - y∈[-4;+∞).
13. График функции на рисунке в приложении.
либо 9+16=25