1) D = R. 2) D = (-∞; 5) U (5; +∞). 3) D = (-∞; -3) U (-3; 2) U (2; +∞). 4) D = (-∞;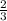 
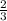) U ( ; +∞). 5) D = (-∞; -3) U (-3; +∞).
Пошаговое объяснение:
Как мы знаем, D = множество аргументов, при котором уравнение имеет смысл.
1) y =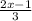 
, и здесь будет D = R (любое число), т.к. делитель всегда будет 3.
2) y =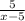 
,
х - 5 ≠ 0;
x ≠ 5.
D = (-∞; 5) U (5; +∞).
3) y =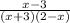 
,
1. х + 3 ≠ 0
2. х ≠ -3.
1. 2 - х ≠ 0.
- х ≠ -2.
х ≠ 2.
D = (-∞; -3) U (-3; 2) U (2; +∞).
4) Корень ликвидируется, т.к. есть степень.
2х-5х+2 ≠ 0.
-3х + 2 ≠ 0.
-3х ≠ -2.
3х ≠ 2.
х ≠ .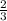
D = (-∞; 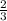) U ( ; +∞).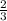
5) 
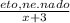, х + 3 ≠ 0.
х ≠ -3.
D = (-∞; -3) U (-3; +∞).
Пошаговое объяснение:
"1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны"
Признаки подобия треугольников.
BD = DC, т.к. они пропорциональны и в целом это два прямоугольных треугольника (рисунок кривой, ну да ладно). AB = AC не стоит объяснять.
Не знаю зачем 1 +, так что уберу их.
BC : BD = BM : AB. Ну, BM = 2x, когда BA = 1х, и BC = 2х, когда BD = 1х. Думаю, я нормально объяснил. Этими теоремами и можно доказать пропорции.
x-1.25x-5.5x=-5,5-12.5-55
7.75x=-73
x=-9,419
У меня так получилось