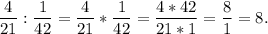Найдите точку максимума функции y=√(-23+14x-x²). ответы 1) 4; 2)-8; 3) 0 ; 4) 7.
Пошаговое объяснение:
В точке максимума функция достигнет наибольшего значения. Если есть предложенные варианты точек просто тупо считаем и выбираем самое большое у.
y(4)=√(-23+14*4-4²)=√(-39+64)=√25=5
y(-8)=√(-23+14*(-8)-(-8)²)=√(-23+112-64)=√25=5
y(0)= не существует ( не можем записывать корень из отрицательного числа)
y(7)=√(-23+14*7-7²)=√(-23+98-49)=√26.
Т.к 26>25 , а значит и √26>√25, то данная функция достигает своего максимума у=√26 при х=7.
Как поделить обыкновенные дроби?
Во втором числе поменяем местами числитель со знаменателем.Деление заменим умножением.Умножаем, как обычные дроби.Как умножать обыкновенные дроби?
Переведём их в дроби без целой части, если они уже переведены, не трогаем.Числитель первой дроби, умножаем на числитель второй дроби;Соответственно знаменатель первой обыкновенной дроби умножаем на знаменатель второй дроби.Затем, если это возможно, сократим, и посмотрим: сокращается ли знаменатель и числитель на одно и то же число. Например: 3/6 = сократима на 3. Значит если сократить на 3, получится 1/2.