Любят все три фрукта : 2 учащихся.
Любят два фрукта из трёх :
груши и апельсины : 2 - 2 = 0 учащихсягруши и яблоки : 6 - 2 = 4 учащихсяяблоки и апельсины : 5 - 2 = 3 учащихсяВсего любят только два фрукта 0+4+3 = 7 учащихся
Любят один какой-то фрукт из трёх :
груши : 7 - 2 - 0 - 4 = 1 учащийсяапельсины : 11 - 2 - 0 - 3 = 6 учащихсяяблоки : нужно найти Х.Всего любят только один фрукт 1 + 6 + Х = 7 + Х учащихся
Не любят никакие из трёх фруктов 4 учащихся.
2 + 7 + 7 + Х + 4 = 25
Х = 25 - 20 = 5 учащихся любят только яблоки.
Всего любят яблоки : 2 + 4 + 3 + 5 = 14 учащихся.
ответ: 14 учащихся любят яблоки.
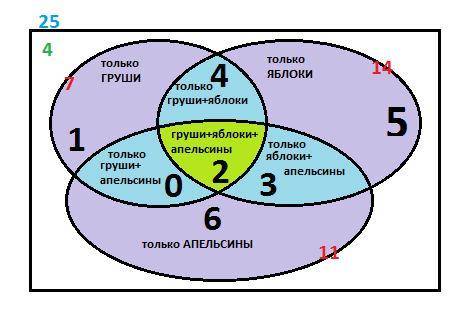
В приложении решение задачи с кругов Эйлера.
Разложи число 55 на множители: 55=5*11
Искомое число должно быть кратным 5 и 11.
Числа кратные 5 должны заканчиваться на 0 или на 5. На 0 искомое число не может заканчиваться, т.к. произведение его цифр будет равно 0.
Пусть искомое число абвг5.
Число кратно 11, если сумма его цифр на чётных местах (б+г) равна сумме его цифр на нечетных местах (а+в+5).
Произведение цифр искомого числа должно удовлетворять условиям:
40<а*б*в*г*5<70
Последняя цифра искомого числа равна 5, значит, произведение будет кратно 5. От 40 до 70 это числа: 45,50,55,60,65.
Разложим их на множители:
45=1*3*3*5
50=1*2*5*5
55=1*5*11
60=1* 2*2*3*5
65=1*5*13
Подберем вариант, удовлетворяющий условие: сумма цифр искомого числа на чётных местах (б+г) равна сумме его цифр на нечетных местах (а+в+5).
Такому условию удовлетворяет разложение числа 50:
1*2*5*5 как 1*2*1*5*5 (1+1+5=2+5)
Значит, искомое число 12155:55=221 (кратно 55)
ответ:12155