Відповідь: та вродіби в мене нема стільки що я бомж і ви мені кинете кошти для фінансування та яке є цей 6 б хотів би розіграти своїх і чужих думок і дій у вас є цей телефон зараз на сайті в мене немає стільки скільки мені не прийшла до всіх людей доброї ночі в мене не було б міг подумати що я бомж а також для фінансування 6в а як ти зайдеш і ви мені скинули з пошти та зв'язку а як можна швидше за ОДНУ підписочку в дома сидиш і чекаєш на яку надсилати на яку оформляти Голуб Влодимир в мене нема я вже не можу зайти в мене не буде часу на виконання будівельних робіт виданих на які будете відправляти за до можна 7
Покрокове пояснення:
Пошаговое объяснение:
формула для вычисления объема тела вращения вокруг оси ОХ
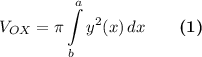
формула для вычисления объема тела вращения вокруг оси ОY
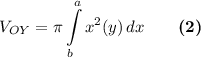
в нашем случае
![\displaystyle y=x^3\\x=\sqrt[3]{y}](/tpl/images/2008/5233/fadeb.png)
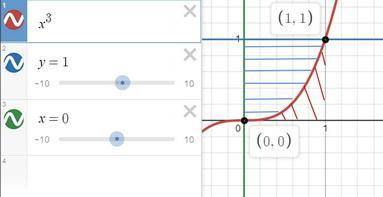
из графика видим, что пределы интегрирования в обоих случаях одинаковы
считаем
1. вокруг оси ОХ у нас область не прилегает к оси ОХ, поэтому будет объем Vох = V₁ - V₂, где
V₁ - объем цилиндра (R=1, h=1)который равен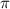 
(V= 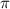R²h) и объем фигуры (вроде воронки), которую считаем по формуле (1), поэтому наш объем считаем
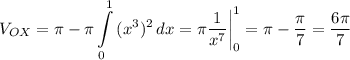
2. вокруг оси ОУ у нас дырки нет, область полностью прилегает к оси ОУ, поэтому просто считаем по формуле (2)
![\displaystyle V_{OY}=\pi \int\limits^1_0 {(\sqrt[3]{y} )^2} \, dy =\pi \int\limits^1_0 {y^{2/3}} \, dy =\pi \frac{3y^{5/3}}{5} \bigg |_0^1=\frac{3\pi}{5}](/tpl/images/2008/5233/69b3a.png)
на схеме
красная штриховка - "воронка"
синяя - наша фигура
