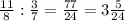
Это дробь 
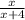 - данная дробь, знаменатель на 4 больше числителя.
- данная дробь, знаменатель на 4 больше числителя.
Если числитель увеличить на 6, а знаменатель на 4, то получим
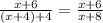 ,
,
то дробь 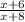 возрастает менее чем вдвое по сравнению с дробью
возрастает менее чем вдвое по сравнению с дробью 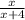
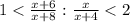
Если же числитель увеличить на 8, а знаменатель на 1,
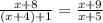
то дробь 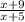 увеличивается более чем втрое по сравнению дробью
увеличивается более чем втрое по сравнению дробью 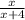
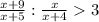
Решаем систему: x≠-4
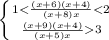
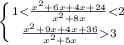

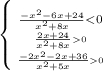
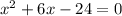
D=132
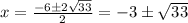
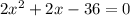
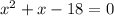
D=1+72
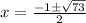
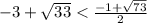
При x=3 получим дробь 
которая удовлетворяет указанным условиям
Если числитель увеличить на 6, а знаменатель на 4, то получим
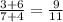 ,
, 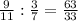 ,
, 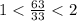
Если же числитель увеличить на 8, а знаменатель на 1,
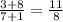
то дробь увеличивается более чем втрое по сравнению дробью
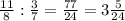
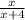 - данная дробь, знаменатель на 4 больше числителя.
- данная дробь, знаменатель на 4 больше числителя.
Если числитель увеличить на 6, а знаменатель на 4, то получим
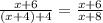 ,
,
то дробь 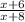 возрастает менее чем вдвое по сравнению с дробью
возрастает менее чем вдвое по сравнению с дробью 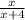
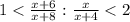
Если же числитель увеличить на 8, а знаменатель на 1,
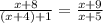
то дробь 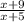 увеличивается более чем втрое по сравнению дробью
увеличивается более чем втрое по сравнению дробью 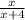
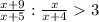
Решаем систему: x≠-4
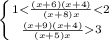
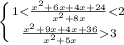

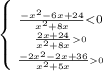
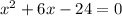
D=132
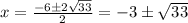
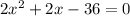
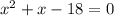
D=1+72
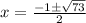
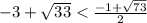
При x=3 получим дробь 
которая удовлетворяет указанным условиям
При x=3 получим дробь 
которая удовлетворяет указанным условиям
Если числитель увеличить на 6, а знаменатель на 4, то получим
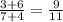 ,
, 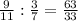 ,
, 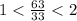
Если же числитель увеличить на 8, а знаменатель на 1,
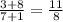
то дробь увеличивается более чем втрое по сравнению дробью