1) Найти области определения и значений данной функции f.
Для аргумента и функции нет ограничений: их значения - вся числовая ось.
2) Выяснить, обладает ли функция особенностями, облегчающими исследование, т. е. является ли функция f: а) четной или нечетной:
f(-x)=(-x)³−1 = -x³−1 = -(x³+1). Значит, функция не чётная и не нечётная.
б) не периодическая.
3) Вычислить координаты точек пересечения графика с осями координат:
- пересечение с осью Оу (х = 0), у = -1.
- пересечение с осью Ох (у = 0), x³−1 = 0, x³ = 1, x = ∛1 = 1.
4) Найти промежутки знакопостоянства функции f.
На основе нулей функции имеем:
- функция отрицательна при х < 1 (x ∈ (-∞; 1),
- функция положительна при х > 1 (x ∈ (1; +∞).
5) на каких промежутках функция f возрастает, а на каких убывает.
Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точка.
Находим производную функции и приравниваем нулю.
y' = 3x² = 0, x = 0 это критическая точка. Находим знаки производной левее и правее этой точки. Так как переменная в квадрате, то знак её положителен. Значит, функция на всей области определения возрастает.
Поэтому не имеет ни минимума, ни максимума.
6) Вторая производная y'' = 6x. Поэтому в точке х = 0 функция имеет перегиб. При x < 0 график функции выпуклый, при x > 0 вогнутый.
7) Асимптот функция не имеет.
60 км расстояние от А до В
Пошаговое объяснение:
Пусть Х количество минут, за которое велосипедист проезжает 1км. Тогда скорость на пути от А до В =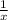 
км/мин. Тогда скорость на пути от А до С, при условии, что он должен проезжать каждый километр на минуту быстрее = 
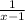км/мин. Время в пути на обоих маршрутах одинаковое 3ч=180минут. Расстояние от А до С больше расстояния от А до В на 30км.
Используя формулу S=V•t, составим уравнение:
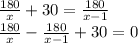умножим каждый член уравнения на 
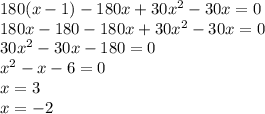не подходит по смыслу задачи
Велосипедист проезжает от А до В 1 км за 3 минуты, значит за 3 часа(180 минут) он проезжает 180 : 3 = 60км
2)мин эй эшен эшлим.
3)салкыннар килде ,кеннэр кыскарды .
4)Мин донья эшен эшлэдем
(Надеюсь ,ты знаешь где поменять букву э и е)