I Бидон + II Бидон + III Бидон =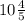 
(1)
I Бидон + II Бидон =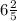 
(2)
данные из (2) подставляем в (1)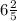 + III Бидон =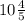
III Бидон =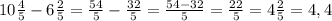 
(л) - молока в третьем бидоне.
==============================================================
I Бидон + II Бидон + III Бидон = 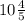(1)
II Бидон + III Бидон =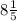 
(2)
данные из (2) подставляем в (1)
I Бидон + =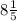
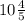
I Бидон =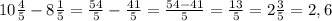 
(л) - молока в первом бидоне.
==============================================================
I Бидон + II Бидон =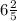
2,6 + II Бидон = 6,4
II Бидон =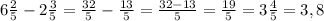 
(л) - молока во втором бидоне.
или II Бидон = 6,4-2,6=3,8 (л) - молока во втором бидоне.
ответ: 2,6 литра молока в первом бидоне; 3,8 литра молока во втором бидоне; 4,4 литра молока в третьем бидоне.
ответ:y=2/(1+x^2)
1) найти область определения функции;
2) исследовать функцию на непрерывность;
3) определить является ли функция четной, нечетной;
4) найти интервалы возрастания, убывания функции и точки ее экстремума;
5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба;
6) найти асимптоты графика функции;
7) построить график функции.
Пошаговое объяснение:
1. Область определения функции (-бесконечность; -корень из 3) ; (-корень из3; корень из3); (корень из 3; бесконечность)
2. Проверим имеет ли функция разрыв в точках х1=корень3 и х2=-корнеь из3
Односторонние пределы в этих точках равны:
lim(х стремиться к корню из3 по недостатку) (x^3/(3(x^2-3)=-бесконечность
lim(х стремиться к корню из3 по избытку) (x^3/(3(x^2-3))=бесконечность
итак в точке х1 функция имеет разрыв второго рода и прямая х=корень из3 является вртикальной асимптотой.
lim(х стремиться к -корню из3 по недостатку) (x^3/(3(x^2-3))=бесконечность
lim(х стремиться к -корню из3 по избытку) (x^3/(3(x^2-3)=-бесконечность
итак в точке х2 функция имеет разрыв второго рода и прямая х=-корень из3 является вертикальной асимптотой.
3. Проверим. является ли данная функция четной или нечетной:
у (х) =x^3/(3(x^2-3))
у (-х) =-x^3/(3(x^2-3)), так как у (-х) =-у (х) , то данная функция нечетная.
4. Найдем точки экстремума функции и промежутки возрастания и убывания:
y'(x)=(x^4-9x^2)/(3(x^2-3)^2); y'(x)=0
(x^4-9x^2)/(3(x^2-3)^2)=0
x^4-9x^2=0
х1=0
х2=3
х3=-3
Получили три стационарные точки, проверим их на экстремум:
Так как на промежутках (-бесконечность; -3) и (3; бесконечность) y'(x)>0, то на этих промежутках функция убывает.
Так как на промежутках (-3; -корень из3) и (-корень из 3;0) и (0; корень из3) и (корень из3;3) y'(x)<0, то на этих промежутках функция убывает.
Так как при переходе через точку х=-3 производная менят свой знак с + на - то в этой точк функция имеет максимум
у (-3)=-4,5
Так ак при переходе черезх тотчку х=3, производная меняет свой знак с - на +, то в этой точке фунция имеет минимум:
у (3)=4,5
Так ка при переходе через точку х=0 производная не меняет сой знак, то в этой точке функция не имеет экстремума.
5. Найдем точки перегиба функции и промежутки выпуклости и вогнутости:
y"(x)=(10x^3+18x)/(x^2-3)^3: y"(x)=0
(10x^3+18x)/(x^2-3)^3=0
х1=0
Так как на промежутках (-бескончность; -корень из3) и (0; корень из3) y"(x)<0, то на этих промежутках график функции направлен выпуклостью вниз
Так как на промежутках (-корень из3;0) и (корень из3; бесконесность) y"(x)>0, то на этих промежутках график функции напрвлен выпуклостью вверх.
Точка х=0 является тоской перегиба.
в 1 и 2б- 6ц 2/5л.
во2 и 3б-8ц1/5 л
всего-10ц4/5л
в каждом б-?л
1) 10ц4/5-6ц2/5=54/5-32/5=22/5=4ц2/5 (л.)-в 3 бидоне
2) 10ц4/5-8ц1/5=54/5-41/5=13/5=2ц3/5 (л.)-в 1 б.
3) 4ц2/5+2ц3/5=22/5+13/5=35/5=7 (л)- в 1 и 3 бидонах
4) 10ц4/5-7=54/5-35/5=19/5=3ц4/5 (л.) -во 2 б
ответ: в 1 бид-2ц3/5 литра, во 2 бидоне-3ц4/5 литра, в 3 бидоне-4ц2/5 литра