(3,6х-х) * 2/3 = 23,4
2,6х * 2/3 = 23,4
х = 23,4 * 3 / 5,2
х = 13,5 км / велосипедист
13,5 * 3,6 = 48,6 км / мотоциклист
ответ; 13,5 км ,48,6 км
Решение без ур-ия
расст. 23,4 км
ск. вел. 13,5 км/час
время 2/3 часа
ск. мото. ? км/час
Решение.
13,5 *(2/3) = (135*2)/(10*3) = 9 (км) такое расстояние еще проедет велосипедист за 2/3 часа
23,4 + 9 = 32,4 (км) всего надо проехать мотоциклисту за 2/3 часа, чтобы догнать велосипедиста
32,4 : (2/3) = (324*3)/(10*2) = 48,6 (км/час) скорость мотоциклиста
ответ: 48,6 км/час
ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
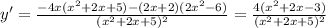
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.