Пошаговое объяснение:
У Вали есть: 6 апельсиновых, 7 клубничных, 6 лимонных и 5 вишневых.
1) Какое самое маленькое количество пакетиков сможет собрать Валя, чтобы ни в одном пакетике не было двух одинаковых конфет и чтобы во всех пакетиках конфет было одинаковое количество. ?
Меньше всего у Вали вишневых конфет - 5 .
Значит наименьшее количество пакетов , в которых количество конфет будет одинаковое и не будет двух одинаковых конфет, будет - 5 пакетиков
2) Всего конфет у Вали
6+7+6+5=24 конфеты
Если их разложили в 8 пакетов , то в каждом пакете было
24:8 = 3 конфеты .
Вишневых конфет 5, значит в 5 пакетах будут вишневые конфеты .
Значит и апельсиновая, и лимонная , и клубничная конфета будут в
8-5=3 пакетах
Основание данной пирамиды - квадрат. ⇒ АВ||СD.
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
АВ || плоскости SCD.
2) Все точки прямой, параллельной плоскости, равноудалены от этой плоскости. ⇒
Расстояние от А до плоскости SCD равно расстоянию от любой точки стороны АВ до плоскости SCD
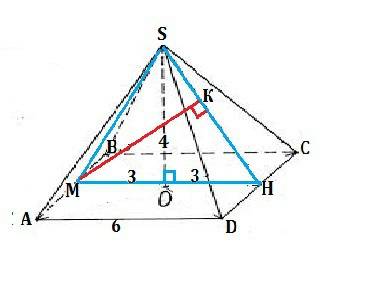
Проведем через высоту пирамиды плоскость МSН ⊥ АВСD и || AD.
Пирамида правильная, все ее апофемы равны,⇒ треугольник МSН - равнобедренный и основание высоты пирамиды лежит в центре квадрата ABCD.
SO=4, OH=3 ⇒ ∆ SOH - египетский, и SH=5 ( можно найти по т.Пифагора)
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость.
Расстояние от А до плоскости SCD равно МК, высоте ∆ МSH, т.е. перпендикуляру, проведенному к SH.
Высоту можем найти из площади треугольника.
Площадь треугольника равна половине произведения длин высоты и стороны, к которой высота проведена.
S. ∆ МSH=SO•MH:2
S. ∆ МSH=4•6:2=12
S∆ MSH=MK•SH:2⇒
MK=2S:SH=2•12:5=4,8 см - это искомое расстояние.
-42х+441+576-72х-29=30х+900+66х+484
-114х+988=96х+1384
-114х-96х=1384-988
-210х=396
х= - 66/35
х= - 1 31/35
-15(15+у)-12(12у+1)+10=16(3у-16)-17(у+17)
-225-15у-144у-12+10=48у-256-17у-289
-227-159у=31у-545
-159у-31у=-545-227
-190у=-318
у= 159/95
у= 1 64/95