В конце марта 1771 года, во время первого путешествия по Италии, Леопольд Моцарт с сыном задержались в Болонье, чтобы познакомиться с падре Мартини. Этот выдающийся композитор, историк и теоретик музыки был членом и фактическим руководителем болонской Филармонической академии, самого известного музыкального института своего времени. Диплом академии открывал двери ко многим престижным и хорошо оплачиваемым должностям. Отец Моцарта постарался устроить знакомство сына с падре Мартини. Мартири сразу же отметил талант Моцарта и с радостью взялся готовить его к экзамену в Филармоническую академию. Три месяца подряд Моцарт ходил к нему каждый день, постигая под его руководством тайны контрапункта и прочие музыкальные премудрости. 9 октября он с успехом сдал экзамен, переработав для четырех партий григорианский антифон «Quaerite primum regnum Dei».
:(
Забегая вперед, скажу, что никаких особенных преимуществ диплом Филармонической академии Моцарту не дал, однако о занятиях с падре Мартини он сохранил самые благодарные воспоминания.
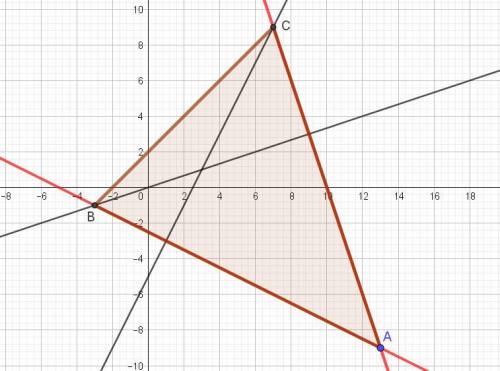
Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
40с=230
с=5,75