ответ и Пошаговое объяснение:
Координаты точки А (10*sqrt(3)/2,10*1/2), так как координата по оси х
это величина ОА , умноженная на косинус 30 градусов, , а координата по оси у,это величина ОА , умноженная на синус 30 градусов.
Значит А(5*sqrt(3),5).
Точно также В(-4*sqrt(3),4).
Найдем длину АВ. Ее квадрат сумма квадратов разностей координат.(5*sqrt(3)+4*sqrt(3))^2+(5-4)^2=3*81+1=244
Значит длина АВ равна 2*sqrt(61)
Периметр АВС равен 8+10+2*sqrt(61)=18)+2*sqrt(61)
Периметр MNP, составленный из средних линий треугольника АВС равен
9+sqrt(61)
Здесь sqrt - корень квадратный, ^ - возведение в степень
Пошаговое объяснение:
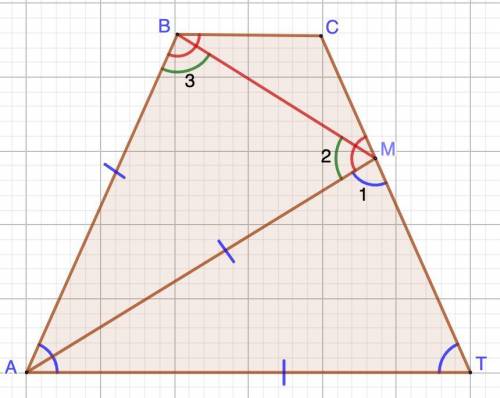
Дано: АВСТ - трапеция
AB=AT=AM=CT
Доказать: ΔВСМ - равнобедренный.
Доказательство:
1. Рассмотрим АВСТ.
АВ = СТ (условие)
⇒ АВСТ - равнобедренная трапеция.
В равнобедренной трапеции углы при основаниях равны.⇒ ∠А = ∠Т.
В трапеции углы, прилежащие к боковой стороне равны в сумме 180°.⇒ ∠В = 180° - ∠А
2. Рассмотрим ΔАМТ.
АТ = АМ (условие)
⇒ ΔАМТ - равнобедренный.
Углы при основании равнобедренного треугольника равны.⇒ ∠Т = ∠1
3. Сумма смежных углов равна 180°.
∠АМС = 180°-∠1 (смежные)
∠В = 180° - ∠А (п.1)
∠А = ∠Т = ∠1 (п.1,2)
⇒ ∠В = ∠АМС
4. Рассмотрим ΔАВМ.
АВ = АМ (условие)
⇒ ΔАВМ - равнобедренный.
⇒ ∠2 = ∠3 (при основании р/б треугольника)
5. Рассмотрим ΔВСМ.
∠МВС = ∠В - ∠3
∠ВМС = ∠АМС-∠2
⇒ ∠МВС = ∠МВС
Если в треугольнике равны два угла, то этот треугольник равнобедренный.⇒ ΔВСМ - равнобедренный.
2) 416/52=8 часов ехал 1 поезд
3)366/61=6 часов ехал 2 поезд
4) 8-6=2 часа